题目内容
3. 已知:如图,在△ABC中,DE∥BC,点F为AD上的一点,且AD2=AB•AF.
已知:如图,在△ABC中,DE∥BC,点F为AD上的一点,且AD2=AB•AF.求证:EF∥CD.
分析 由平行线分线段成比例定理得出$\frac{AD}{AB}$=$\frac{AE}{AC}$,再根据$\frac{AF}{AD}$=$\frac{AD}{AB}$,即可得出$\frac{AE}{AC}$=$\frac{AF}{AD}$,从而得出EF∥DC.
解答 证明:∵DE∥BC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∵AD2=AB•AF,
∴$\frac{AF}{AD}$=$\frac{AD}{AB}$,
∴$\frac{AF}{AD}=\frac{AE}{AC}$,
∴$\frac{AE}{AC}$=$\frac{AF}{AD}$,
∴EF∥DC.
点评 本题考查了平行线分线段成比例.找准对应关系是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
18.在△ABC中,点D为边AC上的一点,∠DBC=∠A,BC=$\sqrt{6}$,AC=3,则CD的长为( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
12.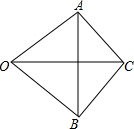 如图所示,OC是∠A0B的平分线,AC⊥AO,BC⊥BO,则OC与AB的关系是( )
如图所示,OC是∠A0B的平分线,AC⊥AO,BC⊥BO,则OC与AB的关系是( )
 如图所示,OC是∠A0B的平分线,AC⊥AO,BC⊥BO,则OC与AB的关系是( )
如图所示,OC是∠A0B的平分线,AC⊥AO,BC⊥BO,则OC与AB的关系是( )| A. | AB垂直平分OC | B. | OC垂直平分AB | ||
| C. | OC只平分AB但不垂直 | D. | OC只垂直AB但不平分 |
13.已知ac2=bc2,下列等式一定成立的是( )
| A. | 2ac2-1=bc2-2 | B. | ac=bc | C. | a=b | D. | ac2+1=bc2-1 |
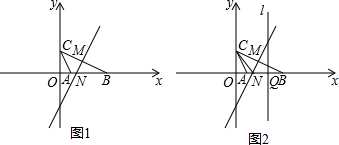
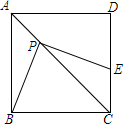 边长为1的正方形ABCD中,点P是对角线AC上一动点(不与点A、C重合),作PE⊥PB交CD于点E.
边长为1的正方形ABCD中,点P是对角线AC上一动点(不与点A、C重合),作PE⊥PB交CD于点E.