Question

15．为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生仅选择一个类别的拓展性课程．为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：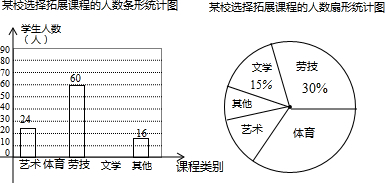

根据统计图中的信息，解答下列问题：
（1）本次被调查的学生人数为200；
（2）将“文学”对应的条形图补充完整；
（3）扇形统计图中“体育”对应的圆心角为126°；
（4）若该校共有1800名学生，请估计全校选择体育类的学生人数．

Answer 1

分析 （1）根据条形统计图和扇形统计图可知选择劳技的学生60人，占总体的30%，从而可以求得调查学生人数；
（2）根据文学的百分比和（1）中求得的学生调查数可以求得文学的有多少人，从而可以求得体育的多少人，进而可以将条形统计图补充完整；
（3）用360度乘以体育类人数占总人数的比例可得；
（4）根据调查的选择体育的学生所占的百分比可以估算出全校选择体育类的学生人数．

解答 解：（1）60÷30%=200（人），
即本次被调查的学生有200人，
故答案为：200；

（2）选择文学的学生有：200×15%=30（人），
选择体育的学生有：200-24-60-30-16=70（人），
补全的条形统计图如下图所示，


（3）扇形统计图中“体育”对应的圆心角为360°×$\frac{70}{200}$=126°，
故答案为：126；

（4）1800×$\frac{70}{200}$=630（人）．
即全校选择体育类的学生有630人．

点评 本题考查条形统计图、用样本估计总体、扇形统计图，解题的关键是明确题意，找出所求问题需要的条件、利用数形结合的思想解答问题．