题目内容
3.阅读下列文字:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.
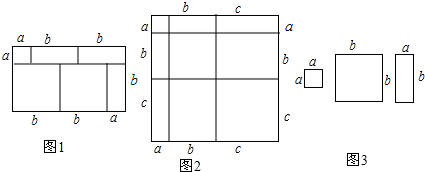
请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,请利用所给的纸片拼出一个长方形,使它的面积为2a2+5ab+2b2,把拼出的图形画在方框内,并拼出的图形将多项式2a2+5ab+2b2分解因式.

分析 (1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.
(2)利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.
(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件.
解答 解:(1)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,
各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,
故等式为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)a2+b2+c2 =(a+b+c)2-2ab-2ac-2bc
=112-2×38
=45.
(3)如图所示:
故2a2+5ab+2b2=(2a+b)(a+2b).
点评 本题考查了因式分解的应用,完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.

练习册系列答案
相关题目
11.在面积为60的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F.若AB=10,BC=12,则CE-CF的值为( )
| A. | 2+$\sqrt{3}$ | B. | 22+11$\sqrt{3}$ | C. | 2-$\sqrt{3}$或22-11$\sqrt{3}$ | D. | 22-11$\sqrt{3}$或22+11$\sqrt{3}$ |
8.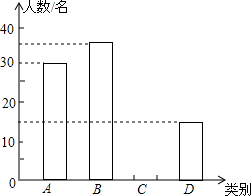 由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
(1)表格中a=15,b=0.3,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“使用电子鞭炮”的学生有多少名?
 由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,某校团委向全校2000多名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | 30 | b |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | a | 0.15 |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“使用电子鞭炮”的学生有多少名?
12.小明的爸爸对小明中考前的6次数学测验成绩进行分析,判断小明的数学成绩是否稳定,则小明的爸爸需要知道这6次数学成绩的( )
| A. | 平均数或中位数 | B. | 众数或平均数 | C. | 方差或标准差 | D. | 极差或众数 |
13. 如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )
如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )
 如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )
如图所示,A为河岸上的码头,B为河中的一只小船,那么这只小船的位置确定方法不能是( )| A. | 以A为原点,河岸为x轴,建立直角坐标系来确定 | |
| B. | 以A为原点,河岸为y轴,建立直角坐标系来确定 | |
| C. | 以AB间的距离和B在A的北偏东若干度来确定 | |
| D. | 以B为原点,平行于河岸的直线为x轴,建立直角坐标系来确定 |