题目内容
2.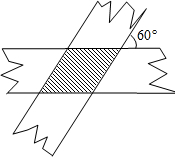 如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )
如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 过A作AE⊥BC于E,AF⊥CD于F,则AE=AF=$\sqrt{3}$,∠AEB=∠AFD=90°,求出四边形ABCD是平行四边形,证出△AEB≌△AFD,推出AB=AD,求出四边形ABCD是菱形,根据菱形的性质得出AB=BC,解直角三角形求出AB,根据菱形的面积公式求出即可.
解答 解: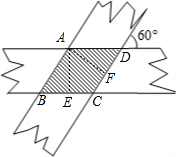
过A作AE⊥BC于E,AF⊥CD于F,
则AE=AF=$\sqrt{3}$,∠AEB=∠AFD=90°,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠ABE=∠ADF=60°,
在△AEB和△AFD中
$\left\{\begin{array}{l}{∠ABE=∠ADF}\\{∠AEB=∠AFD}\\{AE=AF}\end{array}\right.$
∴△AEB≌△AFD,
∴AB=AD,
∴四边形ABCD是菱形,
∴AB=BC,
在Rt△AEB中,∠AEB=90°,AE=$\sqrt{3}$,∠ABE=60°,
∴BE=$\frac{AE}{tan60°}$=1,AB=$\frac{AE}{sin60°}$=2,
∴BC=AB=2,
∴重叠部分的面积是BC×AE=2$\sqrt{3}$,
故选D.
点评 本题考查了平行四边形的判定,菱形的性质和判定,解直角三角形,全等三角形的性质和判定的应用,能求出四边形ABCD是菱形是解此题的关键,难度适中.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
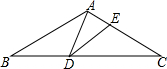 如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.
如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.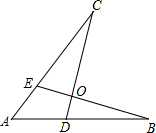 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠ACD=120°,则∠A=30°.
如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠ACD=120°,则∠A=30°.