题目内容
某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为____．
y＝a(1＋x)2
【解析】试题分析：∵一月份新产品的研发资金为a元，
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为，∴三月份的研发资金为．
故答案为： ．
轻巧夺冠周测月考直通中考系列答案如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB.（结果保留整数
）
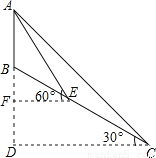
塔高AB大约为58米
【解析】【解析】
依题意可得：∠AEB=30°，∠ACE=15°，
又∵∠AEB=∠ACE+∠CAE，∴∠CAE=15°。
∴△ACE为等腰三角形。∴AE=CE=100米。
在Rt△AEF中，∠AEF=60°，∴EF=AEcos60°=50（米），AF=AEsin60°=50（米）。
在Rt△BEF中，∠BEF=30°，∴BF=EFtan30°... 已知二次函数y=-x2+4x-3，其图象与y轴交于点B，与x轴交于A，C 两点.求△ABC的周长和面积.
C△ABC=，S△ABC=3.
【解析】试题分析：先分别求得二次函数的图象与坐标轴的交点坐标，再根据勾股定理求得△ABC的三边长，即可得到△ABC的周长，再根据三角形的面积公式即可求得结果.
令x=0,得y=-3,故B点坐标为(0,-3).
解方程-x2+4x-3=0,得x1=1,x2=3.
故A、C两点的坐标为(1,0),(3,0).
所以AC=3-1=2,AB=,... 如图，在平面直角坐标系中，O是坐标原点，点A的坐标是(－2，4)，过点A作AB⊥y轴，垂足为B，连接OA.
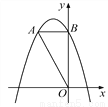
(1)求△OAB的面积；
(2)若抛物线y＝－x2－2x＋c经过点A.
①求c的值；
②将抛物线向下平移m个单位长度，使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界)，求m的取值范围(直接写出答案即可)．
（1）4；（2）①c＝4；②m的取值范围为1＜m＜3.
【解析】（1）根据点A的坐标是（-2，4），得出AB，BO的长度，即可得出△OAB的面积；
（2）①把点A的坐标（-2，4）代入y=-x2-2x+c中，直接得出即可；
②利用配方法求出二次函数解析式即可得出顶点坐标，根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围．
【解析】
（1）∵点A的坐标是（-2，4）... 已知二次函数y＝－x2＋4，当－2≤x≤3时，函数的最小值是_____，最大值是____．
－5 4
【解析】试题解析：抛物线y＝－x2＋4，开口向下，有最大值为4，当x=3时有最小值为-5. 某市烟花厂为该市4.18烟花三月经贸旅游特别设计制作一种新型礼炮，这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h＝－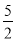
t2＋20t＋1.若这种礼炮点火开空到最高点处引爆，则从点火升空到引爆需要的时间为( )
A. 3s B. 4s C. 5s D. 6s
B
【解析】把二次函数的一般式写成顶点式h=-t2+20t+1=-（t-4）2+41，找出顶点坐标（4，41），当t=4时，升到最高点．
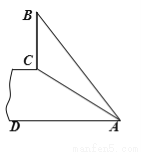
故选：B． 如图，斜坡AC的坡度（坡比）为1: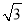 
，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．
6米.
【解析】
试题分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．
试题解析：延长BC交AD于E点，则CE⊥AD．
在Rt△AEC中，AC=10，由坡比为1：可知：∠CAE=30°，
∴... 如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，如果顾客乘地铁从点B到点C上升的高度为5m，则电梯BC的长是（ ）
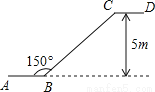
A．5cm B．5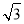
cm C．10m D．
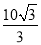m
C．
【解析】
试题分析：如图所示：过点C作CE⊥AB延长线于点E，
∵∠ABC=150°，
∴∠CBE=30°，
∵从点B到点C上升的高度为5m，
∴电梯BC的长是10m．
故选C． 分解因式：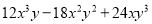 
=6xy（______）
【解析】 =6xy（）.