题目内容
在△ABC中，点D、E在AB上 点F在BC上，EF∥DC，BD2=BE•BA，判断DF与AC的位置关系．
考点：相似三角形的判定与性质
专题：
分析：由条件可证明△BDF∽△BAC，可得角相等，根据平行线的判定可证得DF∥AC．
解答：解：DF∥AC，证明如下：
∵EF∥CD
∴
=
，
又∵BD2=BE•BA，
∴
=
，且∠DBF=∠ABC
∴△BDF∽△BAC，
∴∠BDF=∠A，
∴DF∥AC．
∵EF∥CD
∴
| BE |
| BD |
| BF |
| BC |
又∵BD2=BE•BA，
∴
| BE |
| BD |
| BD |
| AB |
∴△BDF∽△BAC，
∴∠BDF=∠A，
∴DF∥AC．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的对应角相等是解题的关键．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
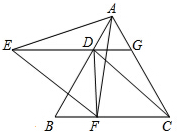如图，△ABC是等边三角形，EG∥BC，DE=DB．EF∥DC，连接DF．
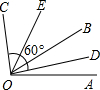如图，∠AOB：∠BOC=3：5，又OD、OE分别是∠AOB和∠BOC的平分线，若∠DOC=60°，求∠AOB和∠BOC的度数．
如图，∠DOE：∠BOE=1：2，∠DOC：∠COA=1：2，如果∠AOB=120°，那么∠EOC是多少度？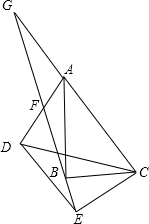
如图，在△ABC和△DEC中，∠ABC=∠DEC=90°，连接AD交射线EB于F，过A作AG∥DE交射线EB于点G，点F恰好是AD中点．