Question

19．函数y=|x-1|（-1≤x≤2）与y=$\frac{1}{2}$x+m的图象有两个交点，则m的取值范围为（　　）

• A． 0＜m≤$\frac{5}{2}$
• B． m=-$\frac{1}{2}$
• C． -$\frac{1}{2}$＜m≤0
• D． -$\frac{1}{2}$≤m≤$\frac{5}{2}$

Answer 1

分析 作出函数图象，求出y=$\frac{1}{2}$x+m恰好经过拐点和两个函数图象有两个交点时的m的值，再写出m的取值范围即可．

解答 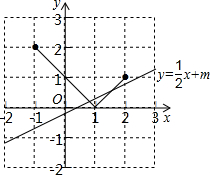解：如图，当y=$\frac{1}{2}$x+m经过点（1，0）时，$\frac{1}{2}$+m=0，
解得m=-$\frac{1}{2}$，
当y=$\frac{1}{2}$x+m经过点（2，1）时，$\frac{1}{2}$×2+m=1，
解得m=0，
所以，两个函数图象有两个交点时，m的取值范围是-$\frac{1}{2}$＜m≤0．
故选C．

点评 本题考查了两直线相交的问题，作出函数图象，利用数形结合的思想求解更形象直观，要注意经过第一个函数图象拐点时只有一个交点．