题目内容
9.在长为3a+2,宽为3a-2的长方形木板上,挖去边长为2a+1的小正方形,求剩余部分的面积.分析 利用长方形的面积减去挖去边长为2a+1的小正方形面积,然后再计算即可.
解答 解:由题意得:
(3a+2)(3a-2)-(2a+1)2,
=9a2-4-(4a2+4a+1),
=9a2-4-4a2-4a-1,
=5a2-4a-5.
答:剩余部分的面积为5a2-4a-5.
点评 此题主要考查了多项式乘法,关键是掌握多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在密码学中,你直接可以看到的内容为明文(真实文),对明进行某种处理后得到的内容为密文.现有一种密码把英文的明文单词按字母分解,其中英文的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数.见以下表格.
现给出一个公式:
x′=$\left\{\begin{array}{l}{\frac{x+1}{2}(x为自然数,1≤x≤26,x不能被2整除)}\\{\frac{x}{2}+13(x为自然数,1≤x≤26,x能被2整除)}\end{array}\right.$
将明文字母对应的数字x按以上公式计算得到密文字母对应的数字x′,比如明文字母为g,g→7→$\frac{7+1}{2}$=4→d,所以明文字母g对应的密文字母为d.
(1)按照上述规定,将明文good译成的密文是什么?写出你的计算过程;
(2)按照上述规定,请你写出由密文字母x′得到明文字母x的公式;
(3)按照②中你得到的公式,密文gawqj所代表的明文单词是什么?(直接写出结果)
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
x′=$\left\{\begin{array}{l}{\frac{x+1}{2}(x为自然数,1≤x≤26,x不能被2整除)}\\{\frac{x}{2}+13(x为自然数,1≤x≤26,x能被2整除)}\end{array}\right.$
将明文字母对应的数字x按以上公式计算得到密文字母对应的数字x′,比如明文字母为g,g→7→$\frac{7+1}{2}$=4→d,所以明文字母g对应的密文字母为d.
(1)按照上述规定,将明文good译成的密文是什么?写出你的计算过程;
(2)按照上述规定,请你写出由密文字母x′得到明文字母x的公式;
(3)按照②中你得到的公式,密文gawqj所代表的明文单词是什么?(直接写出结果)
18.如果x2-x+2的值为7,则-$\frac{1}{2}$x2+$\frac{1}{2}$x+5的值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{15}{2}$ | D. | 答案不唯一 |
19.函数y=|x-1|(-1≤x≤2)与y=$\frac{1}{2}$x+m的图象有两个交点,则m的取值范围为( )
| A. | 0<m≤$\frac{5}{2}$ | B. | m=-$\frac{1}{2}$ | C. | -$\frac{1}{2}$<m≤0 | D. | -$\frac{1}{2}$≤m≤$\frac{5}{2}$ |
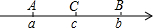 如图,已知数轴上点A,B,C所对应的数a,b,c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,试确定原点O的大致位置.
如图,已知数轴上点A,B,C所对应的数a,b,c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,试确定原点O的大致位置. 如图,边长为m,n的长方形,它的周长为10,面积为6,则m2n+mn2的值为30.
如图,边长为m,n的长方形,它的周长为10,面积为6,则m2n+mn2的值为30.