题目内容
10.若当1<x<2时,不等式$\frac{1}{x}$>m有解,求m的取值范围.分析 根据题意确定$\frac{1}{x}$的范围,得到答案.
解答 解:∵1<x<2,
∴$\frac{1}{2}$<$\frac{1}{x}$<1,
当不等式$\frac{1}{x}$>m有解时,$\frac{1}{2}$<m<1.
点评 本题考查的是不等式的解集的确定,确定$\frac{1}{x}$的范围是解题的关键.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18.如果x2-x+2的值为7,则-$\frac{1}{2}$x2+$\frac{1}{2}$x+5的值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{15}{2}$ | D. | 答案不唯一 |
19.函数y=|x-1|(-1≤x≤2)与y=$\frac{1}{2}$x+m的图象有两个交点,则m的取值范围为( )
| A. | 0<m≤$\frac{5}{2}$ | B. | m=-$\frac{1}{2}$ | C. | -$\frac{1}{2}$<m≤0 | D. | -$\frac{1}{2}$≤m≤$\frac{5}{2}$ |
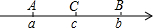 如图,已知数轴上点A,B,C所对应的数a,b,c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,试确定原点O的大致位置.
如图,已知数轴上点A,B,C所对应的数a,b,c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,试确定原点O的大致位置. 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如: