题目内容
11．若直角三角形的三边长分别为a，b，c（其中c为斜边长），则三角形的内切圆半径R=$\frac{a+b-c}{2}$．分析 利用内切圆半径等于两直角边的和与斜边的差的一半，即可计算出内切圆半径．
解答 解：∵直角三角形两条直角边长为a、b，斜边长为c，
∴直角三角形的内切圆半径是：$\frac{a+b-c}{2}$．
故答案为：$\frac{a+b-c}{2}$．
点评 此题考查了三角形的内切圆的知识．解题的关键是掌握直角三角形内切圆半径等于两直角边的和与斜边的差的一半．
练习册系列答案
相关题目
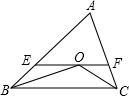已知：如图，∠ABC和∠ACB的平分线交于点O，过点O作EF∥BC，交AB，AC于点E，F．
如图，在四边形ABCD中，点E、F、G分别是AD、BC、BD的中点，AB=CD=6，AD=EF=3$\sqrt{2}$，联结EG、GF、EF，那么△EGF的形状是等腰直角三角形．
如图，在△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为10cm，那么△ABC的周长为16cm．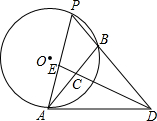
如图，AD切⊙O于A，DBP交⊙O于B，P，C为AB的中点，DC的延长线交AB于E，求证：$\frac{B{D}^{2}}{A{D}^{2}}$=$\frac{AE}{EP}$．