题目内容
 如图,在平面直角坐标系xOy中,点A在x轴的负半轴上,B(5,0),点C在y轴的负半轴上,且OB=OC,抛物线y=x2+bx+c经过A、B、C三点.
如图,在平面直角坐标系xOy中,点A在x轴的负半轴上,B(5,0),点C在y轴的负半轴上,且OB=OC,抛物线y=x2+bx+c经过A、B、C三点.(1)求此抛物线的函数关系式和对称轴;
(2)P是抛物线对称轴上一点,当AP⊥CP时,求点P的坐标;
(3)设E(x,y)是抛物线对称轴右侧上一动点,且位于第四象限,四边形OEBF是以OB为对角线的平行四边形.求?OEBF的面积S与x之间的函数关系式及自变量x的取值范围;当?OEBF的面积为
| 175 |
| 4 |
考点:二次函数综合题
专题:
分析:(1)根据OB=OC求出点C坐标,将B、C坐标代入解析式坐标,求出b,c的值,继而可得出抛物线的函数关系式和对称轴;
(2)设P(2,-m),过点C作CN⊥抛物线对称轴于点N,根据AP⊥CP,利用相似三角形的性质求出点P的坐标;
(3)设点E(x,x2-4x-5),根据平行四边形的性质可得四边形OEBF的面积=2S△OBE,代入可求得?OEBF的面积S与x之间的函数关系式,然后将面积为
代入求出x的值,然后证明四边形OEBF为菱形.
(2)设P(2,-m),过点C作CN⊥抛物线对称轴于点N,根据AP⊥CP,利用相似三角形的性质求出点P的坐标;
(3)设点E(x,x2-4x-5),根据平行四边形的性质可得四边形OEBF的面积=2S△OBE,代入可求得?OEBF的面积S与x之间的函数关系式,然后将面积为
| 175 |
| 4 |
解答:解:(1)由题意,得C(0,-5),
∵抛物线过点B、C,
代入得:
,
解得:
,
∴抛物线的解析式为:y=x2-4x-5,
∴对称轴为直线x=2;
(2)如图1,设P(2,-m)(m>0),
由解析式可得点A坐标为:(-1,0),
设抛物线对称轴交x轴于点M,过点C作CN⊥抛物线对称轴于点N,
∵AP⊥CP,∠AMP=90°,∠PNC=90°,
∴Rt△AMP∽Rt△PNC,
∴
=
,
∴
=
,
解得:m1=2,m2=3,
∴点P1(2,-2),P2(2,-3);

(3)如图2,设点E(x,x2-4x-5),
则S四边形OEBF=2S△OBE=2×
×OB×(-x2+4x+5)=-5x2+20x+25,
其中:2<x<5,
当S四边形OEBF=
时,
代入可得:
=-5x2+20x+25,
∴x1=
,x2=
(舍去),
∵OB=5,点E的横坐标为
,
∴点E在线段OB的中垂线上,
∴OE=BE,
∴平行四边形OEBF是菱形.
∵抛物线过点B、C,
代入得:
|
解得:
|
∴抛物线的解析式为:y=x2-4x-5,

∴对称轴为直线x=2;
(2)如图1,设P(2,-m)(m>0),
由解析式可得点A坐标为:(-1,0),
设抛物线对称轴交x轴于点M,过点C作CN⊥抛物线对称轴于点N,
∵AP⊥CP,∠AMP=90°,∠PNC=90°,
∴Rt△AMP∽Rt△PNC,
∴
| MP |
| CN |
| PN |
| AM |
∴
| m |
| 2 |
| 5-m |
| 3 |
解得:m1=2,m2=3,
∴点P1(2,-2),P2(2,-3);

(3)如图2,设点E(x,x2-4x-5),
则S四边形OEBF=2S△OBE=2×
| 1 |
| 2 |
其中:2<x<5,
当S四边形OEBF=
| 175 |
| 4 |
代入可得:
| 175 |
| 4 |
∴x1=
| 5 |
| 2 |
| 3 |
| 2 |
∵OB=5,点E的横坐标为
| 5 |
| 2 |
∴点E在线段OB的中垂线上,
∴OE=BE,
∴平行四边形OEBF是菱形.
点评:本题考查了二次函数综合题,涉及了利用待定系数法求二次函数的解析式,以及二次函数的对称轴交点坐标的求法等知识.此题难度适中,解题时注意仔细分析题意,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
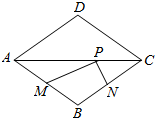 如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是( )
如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是( ) 如图,已知第一象限内的点A在反比例函数
如图,已知第一象限内的点A在反比例函数 如图所示的方格中是美丽可爱的小金鱼,在方格中画出图形向右平移5个格后的图形.
如图所示的方格中是美丽可爱的小金鱼,在方格中画出图形向右平移5个格后的图形. 如图,边长为1的正△ABC,沿EF折叠,使B点落在AC上的点H处,且FH⊥AC,求折成的四边形AEFC的面积.
如图,边长为1的正△ABC,沿EF折叠,使B点落在AC上的点H处,且FH⊥AC,求折成的四边形AEFC的面积. 如图,在10×10的正方形网格中,每个小方格的边长都是1,四边形ABCD的四个顶点在格点上.
如图,在10×10的正方形网格中,每个小方格的边长都是1,四边形ABCD的四个顶点在格点上. 如图,在图中的两个三角形是全等三角形,其中A和D、B和E是对应点.
如图,在图中的两个三角形是全等三角形,其中A和D、B和E是对应点.