题目内容
若a、b、c为△ABC的三边长，且满足a2+b2+c2+200=12a+16b+20c，试判断△ABC的形状并说明理由．
考点：因式分解的应用
专题：
分析：本题通过对式子整理得到a、b、c的值，根据勾股定理的逆定理判定三角形的形状．
解答：解：∵a2+b2+c2+200=12a+16b+20c，
∴（a-6）2+（b-8）2+（c-10）2=0，
∴（a-6）=0，（b-8）=0，（c-10）=0，
∴a=6，b=8，c=10，
∵62+82=102，
∴a2+b2=c2，
∴△ABC是直角三角形．
∴（a-6）2+（b-8）2+（c-10）2=0，
∴（a-6）=0，（b-8）=0，（c-10）=0，
∴a=6，b=8，c=10，
∵62+82=102，
∴a2+b2=c2，
∴△ABC是直角三角形．
点评：本题考查了因式分解的应用．解答此题要用到勾股定理的逆定理．根据勾股定理的逆定理知a2+b2=c2，△ABC是直角三角形．
练习册系列答案
相关题目
若长方形的面积S=6
cm2，长为3
cm，宽为（ ）cm．
| 30 |
| 15 |
A、
| ||
B、2
| ||
C、4
| ||
D、8
|
如图，在平面直角坐标系xOy中，点A在x轴的负半轴上，B（5，0），点C在y轴的负半轴上，且OB=OC，抛物线y=x2+bx+c经过A、B、C三点．
如图，正方形网格中的△ABC，若小方格边长为1，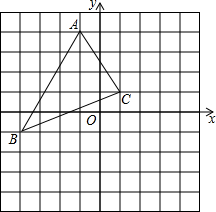
如图，△ABC中，A（-1，4），B（-4，-1），C（1，1），