题目内容
5. 已知b是最小的正整数,且a,b满足(c-5)2+|a+b|=0.请回答题:
已知b是最小的正整数,且a,b满足(c-5)2+|a+b|=0.请回答题:(1)请直接写出a,b,c的值a=-1,b=1,c=5.
(2)图中,a,b,c所对应的点分别为A,B,C,点P为一动点,其对应的数为x,点P在0到2之间运动时,即0≤x≤2时,请化简式子|x+1|-|x-1|+2|x+5|(请写出化简过程).
分析 (1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数的和是0,则每个数是0,即可求得a,b,c的值;
(2)根据x的范围,确定x+1,x-3,5-x的符号,然后根据绝对值的意义即可化简.
解答 解:(1)∵b是最小的正整数,
∴b=1.
根据题意得:$\left\{\begin{array}{l}{c-5=0}\\{a+b=0}\end{array}\right.$,
∴a=-1,b=1,c=5;
(2)∵0≤x≤2,
∴x+1>0,x+5>0,
当0≤x≤1时,x-1≤0,
当1<x≤2时,x-1>0,
∴当0≤x≤1时,|x+1|-|x-1|+2|x+5|=x+1+x-1+2x+10=4x+10.
当1<x≤2时,|x+1|-|x-1|+2|x+5|=x+1-x+1+2x+10=2x+12.
故答案为:(1)-1,1,5.
点评 本题考查了数轴与绝对值:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.用配方法解一元二次方程:-$\sqrt{2}$x2-2x+$\sqrt{6}$=0,可将方程化为( )
| A. | x2+$\sqrt{2}$x=-$\sqrt{3}$ | B. | x2-$\sqrt{2}$x=$\sqrt{3}$ | C. | x2+$\sqrt{2}$x=$\sqrt{3}$ | D. | x2-$\sqrt{2}$x=-$\sqrt{3}$ |
15.($\frac{1}{4}$)2014×42015的结果是( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | 1 | D. | 2 |
 如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°,试探究:四边形AOBC是何种特殊四边形,并给予证明.
如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°,试探究:四边形AOBC是何种特殊四边形,并给予证明. 如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长.
如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长. 如图.在平行四边形ABCD中,AE∥CF,求证:BE=DF.
如图.在平行四边形ABCD中,AE∥CF,求证:BE=DF.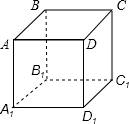 如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.
如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.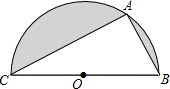 半圆内有一个直角三角形ABC,AB长为a厘米,AC长为b厘米,半圆的半径为r厘米,解答下面各题:
半圆内有一个直角三角形ABC,AB长为a厘米,AC长为b厘米,半圆的半径为r厘米,解答下面各题: