题目内容
12．
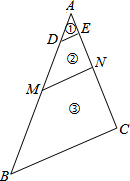如图，DE∥MN∥BC，且AD：DM：MB=1：2：3，则图中△ABC被DE、MN分成的三部分①、②、③的面积之比S①：S②：S③=（ ）| A． | 1：3：6 | B． | 1：4：9 | C． | 1：9：36 | D． | 1：8：27 |
分析 首先根据已知的平行线段，可判定△ADE∽△AFG∽△ABC，进而可由它们的相似比求得面积比，从而得到S①、S②、S③的比例关系．
解答 解：∵AD：DM：MB=1：2：3，
∴AD：AM：AB=1：3：6，
∵DE∥MN∥BC，
∴△ADE∽△AMN∽△ABC，
∴$\frac{{S}_{①}}{{S}_{②}}$=（$\frac{1}{3}$）2=$\frac{1}{9}$，
$\frac{{S}_{①}}{{S}_{③}}$=（$\frac{1}{6}$）2=$\frac{1}{36}$，
∴S①：S②：S③=1：9：36，
故选C．
点评 此题主要考查的是相似三角形的判定和性质，理解相似三角形的面积比等于相似比的平方是解题的关键．
练习册系列答案
相关题目
20．用四舍五入法按要求对1.5268分别取近似值，其中错误的是（ ）
| A． | 1.5（精确到0.1） | B． | 1.5（精确到个位） | ||
| C． | 1.53（保留三个有效数字） | D． | 1.53（精确到0.01） |
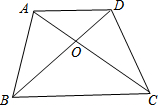梯形ABCD中，AD∥BC，对角线AC、BD交于点O，若AD=3，BC=5，则S△AOD：S△DOC=3：5．