题目内容
4.已知关于x的方程kx2-2(k+1)x+k-1=0有两个不相等的实数根,求k的取值范围.分析 根据方程有两个不相等实数根,则根的判别式△>0,建立关于k的不等式,求得k的取值范围,且二次项系数不为零.
解答 解:(1)∵a=k,b=-2(k+1),c=k-1,
△=b2-4ac=12k+4>0,即k>-$\frac{1}{3}$方程有两个不相等的实数根,
则二次项系数不为零,即k≠0.
∴k的取值范围是:k>-$\frac{1}{3}$且k≠0.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.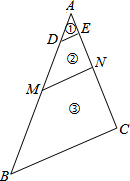 如图,DE∥MN∥BC,且AD:DM:MB=1:2:3,则图中△ABC被DE、MN分成的三部分①、②、③的面积之比S①:S②:S③=( )
如图,DE∥MN∥BC,且AD:DM:MB=1:2:3,则图中△ABC被DE、MN分成的三部分①、②、③的面积之比S①:S②:S③=( )
 如图,DE∥MN∥BC,且AD:DM:MB=1:2:3,则图中△ABC被DE、MN分成的三部分①、②、③的面积之比S①:S②:S③=( )
如图,DE∥MN∥BC,且AD:DM:MB=1:2:3,则图中△ABC被DE、MN分成的三部分①、②、③的面积之比S①:S②:S③=( )| A. | 1:3:6 | B. | 1:4:9 | C. | 1:9:36 | D. | 1:8:27 |
13.已知二次函数y=ax2+2ax+c的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是( )
| A. | (1,0) | B. | (-1,0) | C. | (-3,0) | D. | (3,0) |
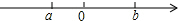 已知实数a,b在数轴上位置如图所示,化简:$\sqrt{{a}^{2}}$+|a-b|=-2a+b.
已知实数a,b在数轴上位置如图所示,化简:$\sqrt{{a}^{2}}$+|a-b|=-2a+b.