题目内容
13. 某水果店新进一种水果,进价为20元/盒,为了摸清行情,决定试营销10天,商家通过这10天的市场调查发现:
某水果店新进一种水果,进价为20元/盒,为了摸清行情,决定试营销10天,商家通过这10天的市场调查发现:①销售价y(元/盒)与销售天数x(天)满足以下关系:
| 天数 | 1≤x≤5 | 6≤x≤10 |
| 销售价格y | $\frac{1}{2}$x+24 | 30 |
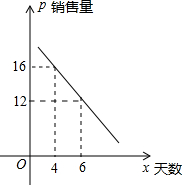
(1)试求每天的销售量p(盒数)与销售天数x之间函数关系式;
(2)设水果店的销售利润为s(元),求销售利润s(元)与销售天数x(天)之间的函数关系式,并求出试营销期间一天的最大利润.
分析 (1)待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”结合x的范围分别求解可得.
解答 解:(1)设销售量p与销售天数x关系式为p=kx+b,
由图象可得$\left\{\begin{array}{l}{4k+b=16}\\{6k+b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=24}\end{array}\right.$,
∴每天的销售量p与销售天数x之间函数关系式为p=-2x+24;
(2)当1≤x≤5时,s=(y-20)p=($\frac{1}{2}$x+24-20)(-2x+24)=-(x-2)2+100,
当x=2时,s取得最大值100;
当6≤x≤10时,s=(y-20)p=(30-20)(-2x+24)=-20x+240,
当x=6时,s取得最大值120;
综上,试营销期间一天的最大利润为120元.
点评 本题主要考查二次函数的应用,根据x的范围分情况得到s关于x的函数解析式及熟练掌握二次函数和一次函数的性质是解题的关键.

练习册系列答案
相关题目
8.2016年11月10日,记者从民政部召开的会议了解到,目前全国农村留守儿童数量为902万人,“902万”用科学记数法表示为( )
| A. | 9.02×102 | B. | 9.02×105 | C. | 9.02×106 | D. | 9.02×104 |
 小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况. 如图:△ABC中,AB=AC,内切圆⊙O与边BC、AB分别切于点D、E、F,若∠C=30°,CE=2$\sqrt{3}$,则AC=4.
如图:△ABC中,AB=AC,内切圆⊙O与边BC、AB分别切于点D、E、F,若∠C=30°,CE=2$\sqrt{3}$,则AC=4.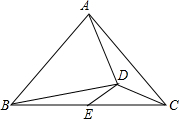 如图,在△ABC中,AB=AC,∠BAC=90°,点D在△ABC内部,AB=BD,AD=$\sqrt{2}$CD,E为BC边的中点,连接DE,若S△ACD=1,则线段DE的长为1.
如图,在△ABC中,AB=AC,∠BAC=90°,点D在△ABC内部,AB=BD,AD=$\sqrt{2}$CD,E为BC边的中点,连接DE,若S△ACD=1,则线段DE的长为1.