题目内容
3.已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.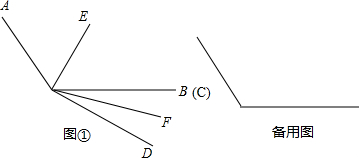
(1)如图①,当OB、OC重合时,求∠AOE-∠BOF的值;
(2)当∠COD从图①所示位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE-∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
分析 (1)首先根据角平分线的定义求得∠AOE和∠BOF的度数,然后根据∠AOE-∠BOF求解;
(2)首先由题意得∠BOC=3t°,再根据角平分线的定义得∠AOC=∠AOB+3t°,∠BOD=∠COD+3t°,然后由角平分线的定义得∠AOE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(110°+3t°)、∠BOF=$\frac{1}{2}$∠BOD=$\frac{1}{2}$(40°+3t°),最后根据∠AOE-∠BOF求解可得;
解答 解:(1)∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×110°=55°,∠BOF=$\frac{1}{2}$∠COD=$\frac{1}{2}$×40°=20°,
∴∠AOE-∠BOF=55°-20°=35°;
(2)∠AOE-∠BOF的值是定值,
如图2,
由题意∠BOC=3t°,
则∠AOC=∠AOB+3t°,∠BOD=∠COD+3t°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(110°+3t°),∠BOF=$\frac{1}{2}$∠BOD=$\frac{1}{2}$(40°+3t°),
∴∠AOE-∠BOF=$\frac{1}{2}$(110°+3t°)-$\frac{1}{2}$(40°+3t°)=35°,
∴∠AOE-∠BOF的值是定值.
点评 本题考查了角度的计算以及角的平分线的性质,理解角度之间的和差关系是关键.

练习册系列答案
相关题目
12.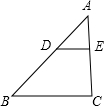 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AE=3,EC=6,则$\frac{AD}{AB}$的值为( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AE=3,EC=6,则$\frac{AD}{AB}$的值为( )
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AE=3,EC=6,则$\frac{AD}{AB}$的值为( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AE=3,EC=6,则$\frac{AD}{AB}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
13.下列说法中正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 圆心角是圆周角的2倍 | |
| C. | 三角形的外心到三角形各边的距离相等 | |
| D. | 从圆外一点可以引圆的两条切线,这一点和圆心的连线平分两条切线的夹角 |
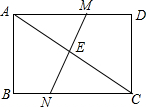 如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N.
如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N. 圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )
圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )


