题目内容
10.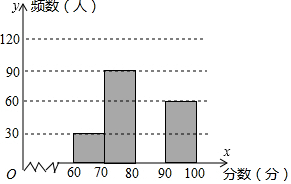 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:| 组别 | 分数段(分) | 频数 | 频率 |
| A组 | 60≤x<70 | 30 | 0.1 |
| B组 | 70≤x<80 | 90 | n |
| C组 | 80≤x<90 | m | 0.4 |
| D组 | 90≤x<100 | 60 | 0.2 |
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在C组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.
分析 (1)先根据A组频数及其频率求得总人数,再根据频率=频数÷总人数可得m、n的值;
(2)根据(1)中所求结果即可补全频数分布直方图;
(3)根据中位数的定义即可求解;
(4)画树状图列出所有等可能结果,再找到抽中A、C的结果,根据概率公式求解可得.
解答 解:(1)∵本次调查的总人数为30÷0.1=300(人),
∴m=300×0.4=120,n=90÷300=0.3,
故答案为:120,0.3;
(2)补全频数分布直方图如下:
(3)由于共有300个数据,则其中位数为第150、151个数据的平均数,
而第150、151个数据的平均数均落在C组,
∴据此推断他的成绩在C组,
故答案为:C;
(4)画树状图如下:
由树状图可知,共有12种等可能结果,其中抽中A﹑C两组同学的有2种结果,
∴抽中A﹑C两组同学的概率为$P=\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,也考查列表法或画树状图法求概率.

练习册系列答案
相关题目
20.下列运算正确的是( )
| A. | a6÷a2=a4 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a2+2a2=3a4 |
5.下列命题的逆命题是假命题的是( )
| A. | 对顶角相等 | |
| B. | 角平分线上的点到这个角的两边的距离相等 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 同旁内角互补,两直线平行 |
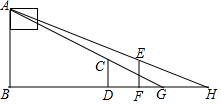 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB. 如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.
如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.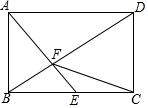 如图,在矩形ABCD中,AB=$\sqrt{2}$,E是BC的中点,AE⊥BD于点F,则CF的长是$\sqrt{2}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,E是BC的中点,AE⊥BD于点F,则CF的长是$\sqrt{2}$. 如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.
如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.