题目内容
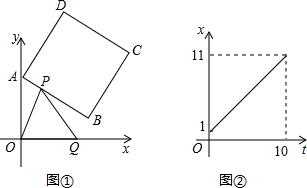
14．
如图，菱形ABCD中，∠BAD=45°，E，F，P分别是AB，BC，AC上的动点，PE+PF的最小值等于2，则AB=2$\sqrt{2}$．
分析 先找出点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，根据轴对称确定最短路线问题以及垂线段最短可知E′F为PE+PF的最小值的最小值，过点B作BG⊥AD于G，解直角三角形求出AB即可．
解答 解：如图，点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，
则PE+PF=E′F为最小值的情况，
过点B作BG⊥AD于G，易知BG=FE′=2，
在Rt△ABG中，∠BAG=45°，
∴AB=BG÷sin45°=2$\sqrt{2}$，
故答案为2$\sqrt{2}$．
点评 本题考查了轴对称确定最短路线问题，菱形的性质，作出图形，确定出最短路线为菱形的对边的距离是解题的关键．
练习册系列答案
相关题目
10．
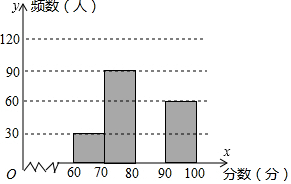为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：
（1）在表中：m=120，n=0.3；
（2）补全频数分布直方图；
（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在C组；
（4）4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．
为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：| 组别 | 分数段（分） | 频数 | 频率 |
| A组 | 60≤x＜70 | 30 | 0.1 |
| B组 | 70≤x＜80 | 90 | n |
| C组 | 80≤x＜90 | m | 0.4 |
| D组 | 90≤x＜100 | 60 | 0.2 |
（2）补全频数分布直方图；
（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在C组；
（4）4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．
5．一中学有学生3000名，2016年母亲节，晓彤为了调查本校大约有多少学生知道自己母亲的生日，随机调查了200名学生，有20名同学不知道自己母亲生日，关于这个数据收集和处理的问题，下列说法错误的是（ ）
| A． | 个体是该校每一位学生 | |
| B． | 本校约有300名学生不知道自己母亲的生日 | |
| C． | 调查的方式是抽样调查 | |
| D． | 样本是随机调查的200名学生是否知道自己母亲的生日 |
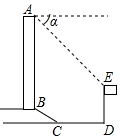如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i=1：$\sqrt{3}$，求大楼AB的高度是多少？（精确到0.1米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{6}$≈2.45）
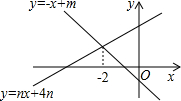如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2，则关于x的不等式-x+m＞nx+4n＞0的整数解为（ ）
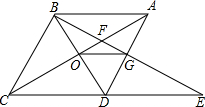如图，在菱形ABCD中，∠BAC=60°，AC与BC交于点O，E为CD延长线上的一点，且CD=DE，连接BE分别交AC、AD于点F、G，连接OG，则下列结论中一定成立的是①④．（把所有正确结论的序号都填在横线上）
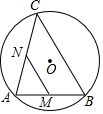如图，AB是⊙O的弦，AB=5，点C是⊙O上的一个动点，且∠ACB=45°，若点M、N分别是AB、AC的中点，则MN长的最大值是$\frac{5\sqrt{2}}{2}$．