题目内容
9.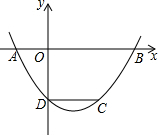 如图,抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A、B,与y轴交于点D,CD∥x轴.与抛物线交于点C,若点A的坐标为(-1,0).则线段OB与线段CD的长度的和为9.
如图,抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A、B,与y轴交于点D,CD∥x轴.与抛物线交于点C,若点A的坐标为(-1,0).则线段OB与线段CD的长度的和为9.
分析 由根与系数的关系可求点B坐标,确定OB长度,把x=c代入可求点C坐标,确定CD长度,即可求解.
解答 解:抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A(-1,0),
∴ax2-4ax+c=0的一根为:x=-1,
可求两根之和等于4,所以方程另一根为:x=5,
∴B(5,0),OB=5,
当x=c时,ax2-4ax+c=c,解得:x=0,或x=4,
∴点C(4,c),
∴CD=4,
∴OB+CD=9.
故答案为:9.
点评 此题主要考查抛物线与直线的交点问题,会把坐标代入抛物线进行分析,会用根与系数的关系进行解题是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.计算|-5|+(π-3.14)0-($\frac{1}{2}$)-1的结果是( )
| A. | 0 | B. | 1 | C. | 4 | D. | 6.5 |
15.下列命题中的假命题是( )
| A. | 等腰三角形的顶角一定是锐角 | |
| B. | 等腰三角形的底角一定是锐角 | |
| C. | 等腰三角形至少有两个角相等 | |
| D. | 等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合 |
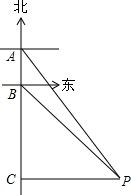 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)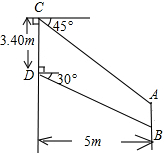 我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)