题目内容
13.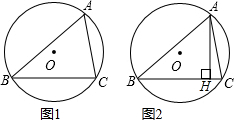 如图1,锐角△ABC内接于⊙O,∠BAC=60°,若⊙O的半径为2$\sqrt{3}$.
如图1,锐角△ABC内接于⊙O,∠BAC=60°,若⊙O的半径为2$\sqrt{3}$.(1)求BC的长度;
(2)如图2,过点A作AH⊥BC于点H,若AB+AC=12,求AH的长度.
分析 (1)首先连接OB,OC,过点O作OD⊥BC于点D,由圆周角定理,即可求得∠BOC的度数,继而求得∠OBC的度数,然后由三角函数的性质,求得BD的长,继而求得答案;
(2)设点G为此三角形ABC内切圆的圆心(角平分线的交点),过G分别向AB,AC,BC作垂线GM,GN,GQ,根据角平分线的性质可知GM=GN=GQ,CQ=CN,BQ=BM,AM=AN,故AM+AN=AB+AC-BC=6,AM=AN=3.在Rt△AGM中,根据锐角三角函数的定义得出GM的长,再由S△ABC=$\frac{1}{2}$BC•AH=S△ABQ+S△BCQ+S△ACQ即可得出结论.
解答 解:(1)连接OB,OC,过点O作OD⊥BC于点D,
∴BD=CD=$\frac{1}{2}$BC,
∵∠A=60°,
∴∠BOC=2∠A=120°,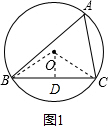
∵OB=OC,
∴∠OBC=∠OCB=$\frac{180°-∠BOC}{2}$=30°,
∵OB=2$\sqrt{3}$,
∴BD=OB•cos30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∴BC=2BD=6.
(2)设点G为此三角形ABC内切圆的圆心(角平分线的交点),过G分别向AB,AC,BC作垂线GM,GN,GQ,
∵GM=GN=GQ,CQ=CN,BQ=BM,AM=AN,
∴AM+AN=AB+AC-BC=6,
∴AM=AN=3.
在Rt△AGM中,
∵∠GAM=30°,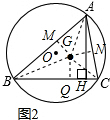
∴S△ABC=$\frac{1}{2}$BC•AH=S△ABQ+S△BCQ+S△ACQ
=$\frac{1}{2}$AB•GM+$\frac{1}{2}$BC•GQ+$\frac{1}{2}$AC•GM
=$\frac{1}{2}$GM(AB+AC+CB)
=9$\sqrt{3}$,
∴AH=3$\sqrt{3}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $(\frac{4}{5}b+a)$元 | B. | $(\frac{5}{4}b+a)$元 | C. | (5b+a)元 | D. | (5a+b)元 |
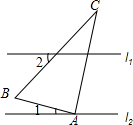 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\sqrt{2}$是2的一个平方根 | B. | -$\sqrt{2}$的平方是2 | ||
| C. | 2的平方根就是2的算术平方根 | D. | $\sqrt{2}$是2的算术平方根 |
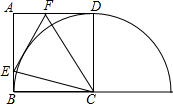 如图,在正方形ABCD中,E是AB边上任意一点,∠ECF=45°,CF交AD于点F,判断直线EF与以C为圆心,CD为半径的圆的位置关系并说明理由.
如图,在正方形ABCD中,E是AB边上任意一点,∠ECF=45°,CF交AD于点F,判断直线EF与以C为圆心,CD为半径的圆的位置关系并说明理由.