Question

19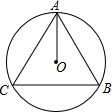．如图，△ABC的三个顶点都在圆O上，AO是∠BAC的角平分线，下列说法一定成立的是（　　）

• A． △ABC是等腰三角形，且AC=BC
• B． △ABC是等腰三角形，且AC=AB
• C． △ABC是等腰三角形，且AB=BC
• D． △ABC是等腰三角形

Answer 1

分析 首先延长AO⊙O于点D，由AO是∠BAC的角平分线，利用圆周角定理证得：$\widehat{CD}$=$\widehat{BD}$，继而证得$\widehat{AC}$=$\widehat{AB}$，即可得AC=AB．

解答 解：延长AO⊙O于点D，
∵AO是∠BAC的角平分线，
∴$\widehat{CD}$=$\widehat{BD}$，
∴$\widehat{AC}$=$\widehat{AB}$，
∴AC=AB．
故选B．

点评 此题考查了圆周角定理以及弧与弦的关系．注意准确作出辅助线是解此题的关键．