题目内容
7．△ABC中，∠C=90°，CA=12cm，CB=16cm，则AB=20cm，高CD=$\frac{48}{5}$cm．分析 直接根据勾股定理求出AB的长，再由三角形的面积公式即可得出高此点的长．
解答 解：∵△ABC中，∠C=90°，CA=12cm，CB=16cm，
∴AB=$\sqrt{{12}^{2}+{16}^{2}}$=20cm，
∴CD=$\frac{CA•CB}{AB}$=$\frac{12×16}{20}$=$\frac{48}{5}$cm．
故答案为：20，$\frac{48}{5}$．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
17．a（x-y）与ay-ax的公因式是（ ）
| A． | a（x-y） | B． | ay+ax | C． | a | D． | x-y |
19．
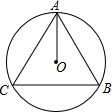如图，△ABC的三个顶点都在圆O上，AO是∠BAC的角平分线，下列说法一定成立的是（ ）
如图，△ABC的三个顶点都在圆O上，AO是∠BAC的角平分线，下列说法一定成立的是（ ）| A． | △ABC是等腰三角形，且AC=BC | B． | △ABC是等腰三角形，且AC=AB | ||
| C． | △ABC是等腰三角形，且AB=BC | D． | △ABC是等腰三角形 |
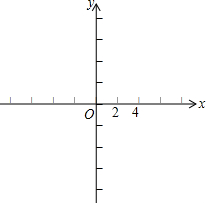如图，在下面的平面直角坐标系中，作出以A（1，2），B（3，1），C（4，4）为顶点的三角形，并在第一象限内作出它的位似三角形A′B′C′，使原三角形与新三角形的位似比为2：1，位似中心是圆点．