题目内容
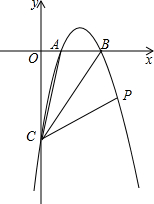 如图:抛物线y=-x2+4x-3与x轴交于A、B两点,与y轴交于C点,点P在抛物线上∠ACB=∠BCP,求P点的坐标.?
如图:抛物线y=-x2+4x-3与x轴交于A、B两点,与y轴交于C点,点P在抛物线上∠ACB=∠BCP,求P点的坐标.?考点:抛物线与x轴的交点
专题:
分析:过点C作CE⊥y轴,过点P作PD⊥CE交CE于点D,由抛物线y=-x2+4x-3与x轴交于A、B两点,可得A,B的坐标,进而得出OA=1,OB=3,由∠BCO=45°,得∠BCD=45°,由∠ACB=∠BCP,可得∠PCD=∠ACO,由tan∠ACO=
,可得tan∠PCD=
,设点P(x,-x2+4x-3),可得PD,CD的值,所以
=
,解得x=
,即可得出点P的坐标.
| 1 |
| 3 |
| 1 |
| 3 |
| -x2+4x |
| x |
| 1 |
| 3 |
| 11 |
| 3 |
解答:解:过点C作CE⊥y轴,过点P作PD⊥CE交CE于点D,
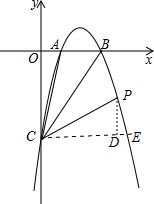
∵抛物线y=-x2+4x-3与x轴交于A、B两点,
∴A的坐标为(1,0),B(3,0)
∴OA=1,OB=3,
令-x2+4x-3=0得C(0,-3),
∴OC=3,
∴∠BCO=45°,
∴∠BCD=45°
∵∠ACB=∠BCP,
∴∠PCD=∠ACO,
∵tan∠ACO=
=
,
∴tan∠PCD=
=
,
设点P(x,-x2+4x-3),
PD=-x2+4x-3+3=-x2+4x,CD=x,
∴
=
,解得x=
,
∴P(
,-
),

∵抛物线y=-x2+4x-3与x轴交于A、B两点,
∴A的坐标为(1,0),B(3,0)
∴OA=1,OB=3,
令-x2+4x-3=0得C(0,-3),
∴OC=3,
∴∠BCO=45°,
∴∠BCD=45°
∵∠ACB=∠BCP,
∴∠PCD=∠ACO,
∵tan∠ACO=
| OA |
| OC |
| 1 |
| 3 |
∴tan∠PCD=
| PD |
| CD |
| 1 |
| 3 |
设点P(x,-x2+4x-3),
PD=-x2+4x-3+3=-x2+4x,CD=x,
∴
| -x2+4x |
| x |
| 1 |
| 3 |
| 11 |
| 3 |
∴P(
| 11 |
| 3 |
| 16 |
| 9 |
点评:本题主要考查了抛物线与x轴的交点,解题的关键是正确作出辅助线,运用正切求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点A在函数y=
如图,点A在函数y=| k |
| x |
| A、-6 | B、-3 | C、3 | D、6 |
 如图,在边长为6
如图,在边长为6 已知a,b在数轴上的位置,如图.
已知a,b在数轴上的位置,如图.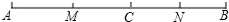 如图,点C在线段AB上,点M,N分别是AC,BC的中点,且AB=14cm.
如图,点C在线段AB上,点M,N分别是AC,BC的中点,且AB=14cm.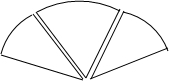 如图为一扇木门上的三块扇形玻璃,已知它们的半径相同,而圆心角分别是40°,60°,40°,每块玻璃均由金属边包裹,而所用金属边总长度为228cm.
如图为一扇木门上的三块扇形玻璃,已知它们的半径相同,而圆心角分别是40°,60°,40°,每块玻璃均由金属边包裹,而所用金属边总长度为228cm.