题目内容
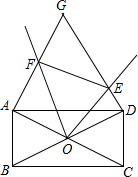 如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.
如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.(1)求证:DE+AF=EF;
(2)若AB=1cm,求△EFG的周长.
考点:相似三角形的判定与性质,矩形的性质
专题:
分析:(1)如图,作辅助线;证明△AOH≌△DOE,得到OH=OE,∠AOH=∠DOE;证明△HOF≌△EOF(SAS),得到HF=EF,故DE+AF=EF,即可解决问题.
(2)求出AD的长度;运用(1)中的结论得到△EFG的周长=AG+DG=2
,即可解决问题.
(2)求出AD的长度;运用(1)中的结论得到△EFG的周长=AG+DG=2
| 3 |
解答: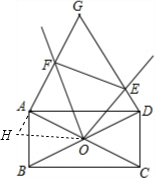 解:(1)如图,延长FA到H,使AH=DE,连接OH;
解:(1)如图,延长FA到H,使AH=DE,连接OH;
∵△ADG为等边三角形,且∠AOD=120°,
∴∠G=60°,∠AOD+∠G=180°,
∴A、O、D、G四点共圆,
∴∠HAO=∠EDO;而四边形ABCD为矩形,
∴OA=OD;
在△AOH与△DOE中,
,
∴△AOH≌△DOE(SAS),
∴OH=OE,∠AOH=∠DOE,
∴∠HOF=∠AOF+∠DOE=120°-∠EOF=60°,
∴∠HOF=∠EOF;
在△HOF与△EOF中,
,
∴△HOF≌△EOF(SAS),
∴HF=EF,即DE+AF=EF.
(2)∵OA=OB,∠AOB=120°,
∴∠OAD=∠ODA=
=30°,
∵∠BAD=90°,AB=1,
∴AD=
,AG=DG=AD=
;
∵DE+AF=EF,
∴△EFG的周长=AG+DG=2
.
 解:(1)如图,延长FA到H,使AH=DE,连接OH;
解:(1)如图,延长FA到H,使AH=DE,连接OH;∵△ADG为等边三角形,且∠AOD=120°,
∴∠G=60°,∠AOD+∠G=180°,
∴A、O、D、G四点共圆,
∴∠HAO=∠EDO;而四边形ABCD为矩形,
∴OA=OD;
在△AOH与△DOE中,
|
∴△AOH≌△DOE(SAS),
∴OH=OE,∠AOH=∠DOE,
∴∠HOF=∠AOF+∠DOE=120°-∠EOF=60°,
∴∠HOF=∠EOF;
在△HOF与△EOF中,
|
∴△HOF≌△EOF(SAS),
∴HF=EF,即DE+AF=EF.
(2)∵OA=OB,∠AOB=120°,
∴∠OAD=∠ODA=
| 180°-120° |
| 2 |
∵∠BAD=90°,AB=1,
∴AD=
| 3 |
| 3 |
∵DE+AF=EF,
∴△EFG的周长=AG+DG=2
| 3 |
点评:该题主要考查了矩形的性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线,构造全等三角形,灵活运用矩形的性质、全等三角形的判定及其性质来分析‘、判断、解答.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目

 如图所示,已知点A、B、C、O分别表示有理数a,b,c,0,试判断下列各式的符号:
如图所示,已知点A、B、C、O分别表示有理数a,b,c,0,试判断下列各式的符号: 如图,在边长为6
如图,在边长为6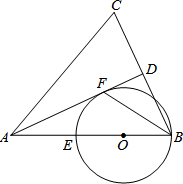 已知:如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.
已知:如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F. 已知a,b在数轴上的位置,如图.
已知a,b在数轴上的位置,如图. 如图,将△ABC沿CA方向平移CA长度得到△EFA,连接BE,其中AB=AC,已知△ABE的面积为3.
如图,将△ABC沿CA方向平移CA长度得到△EFA,连接BE,其中AB=AC,已知△ABE的面积为3.