题目内容
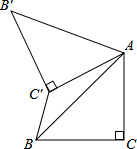 如图,已知△ABC中,∠C=90°,AC=BC=
如图,已知△ABC中,∠C=90°,AC=BC=| 2 |
| A、15° | B、20° |
| C、30° | D、45° |
考点:旋转的性质
专题:
分析:如图,作辅助线;证明△ABB′为等边三角形,此为解决问题的关键性结论;证明△BB′C′≌△BAC,得到∠B′BC′=∠ABC′,即可解决问题.
解答: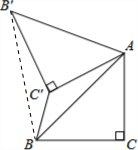 解:如图,连接BB′;由题意得:
解:如图,连接BB′;由题意得:
AB=AB′,∠BAB′=60°,
∴△ABB′为等边三角形,
∴∠B′BA=60°,BB′=BA;
在△BB′C′与△BAC中,
,
∴△BB′C′≌△BAC(SSS),
∴∠B′BC′=∠ABC′=30°,
故选C.
 解:如图,连接BB′;由题意得:
解:如图,连接BB′;由题意得:AB=AB′,∠BAB′=60°,
∴△ABB′为等边三角形,
∴∠B′BA=60°,BB′=BA;
在△BB′C′与△BAC中,
|
∴△BB′C′≌△BAC(SSS),
∴∠B′BC′=∠ABC′=30°,
故选C.
点评:该题主要考查了旋转变换的性质、全等三角形的判定及其性质的应用等几何知识点问题.解题的关键是作辅助线;灵活运用旋转变换的性质、全等三角形的判定来分析、解答.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图所示,已知点A、B、C、O分别表示有理数a,b,c,0,试判断下列各式的符号:
如图所示,已知点A、B、C、O分别表示有理数a,b,c,0,试判断下列各式的符号: 已知a,b在数轴上的位置,如图.
已知a,b在数轴上的位置,如图.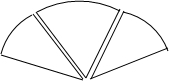 如图为一扇木门上的三块扇形玻璃,已知它们的半径相同,而圆心角分别是40°,60°,40°,每块玻璃均由金属边包裹,而所用金属边总长度为228cm.
如图为一扇木门上的三块扇形玻璃,已知它们的半径相同,而圆心角分别是40°,60°,40°,每块玻璃均由金属边包裹,而所用金属边总长度为228cm.
 如图,将△ABC沿CA方向平移CA长度得到△EFA,连接BE,其中AB=AC,已知△ABE的面积为3.
如图,将△ABC沿CA方向平移CA长度得到△EFA,连接BE,其中AB=AC,已知△ABE的面积为3. 如图,∠1的同旁内角是
如图,∠1的同旁内角是