题目内容
17.A市为解决农村饮用水问题,2008年投入600万元用于“改水工程”,且计划以后每年以相同的增长率投资.若2010年该市计划投资“改水工程”1176万元,请解答下列问题:(1)求A市投资“改水工程”的年平均增长率是多少;
(2)从2008年到2010年,A市三年共投资“改水工程”多少万元?
分析 (1)设两年平均增长率为x,则2009年的投资为:600(1+x),则2010年的投资为:600(1+x)2,进而得出等式求出答案;
(2)利用(1)中所求,进而求出三年投资“改水工程”的总钱数.
解答 解:(1)设A市投资“改水工程”年平均增长率是x,则
600(1+x)2=1176,
解得:x1=0.4,x2=-2.4(不合题意,舍去).
所以,A市投资“改水工程”年平均增长率为40%.
(2)由题意可得:600+600×1.4+1176=2616(万元),
答:A市三年共投资“改水工程”2616万元.
点评 此题主要考查了一元二次方程的应用,正确求出平均增长率是解题关键.

练习册系列答案
相关题目
5.某人去水果批发市场采购苹果,他看中了A、B两家苹果,这两家苹果品质一样,零售价为6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
(1)如果他批发600千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
| 数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
12.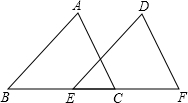 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BE=FC | C. | ∠ACB=∠F | D. | AC=DF |
2.北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:

如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )

如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )
| A. | 汉城与纽约的时差为13小时 | B. | 北京与纽约的时差为13小时 | ||
| C. | 北京与纽约的时差为14小时 | D. | 北京与多伦多的时差为14小时 |
6.下列汽车标志中,是轴对称图形的个数有( )个.


| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
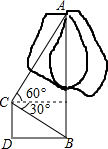 为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)
为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)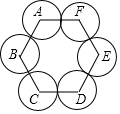 如图,以正六边形的顶点为圆心,1cm为半径的六个圆中,相邻两圆外切,则该正六边形与六个圆重叠部分的面积是2πcm2.
如图,以正六边形的顶点为圆心,1cm为半径的六个圆中,相邻两圆外切,则该正六边形与六个圆重叠部分的面积是2πcm2. 点P是Rt△ABC的斜边AB上异于A、B的一点,过P点作直线PE截△ABC,使截得的三角形与△ABC相似,请你在图中画出满足条件的直线,并标出必要的标记.
点P是Rt△ABC的斜边AB上异于A、B的一点,过P点作直线PE截△ABC,使截得的三角形与△ABC相似,请你在图中画出满足条件的直线,并标出必要的标记.