题目内容
8.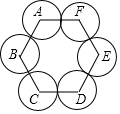 如图,以正六边形的顶点为圆心,1cm为半径的六个圆中,相邻两圆外切,则该正六边形与六个圆重叠部分的面积是2πcm2.
如图,以正六边形的顶点为圆心,1cm为半径的六个圆中,相邻两圆外切,则该正六边形与六个圆重叠部分的面积是2πcm2.
分析 根据多边形的内角和的计算公式求出六边形的内角和,根据扇形的面积公式计算即可.
解答 解:六边形的内角和为:(6-2)×180°=720°,
即∠A+∠B+∠C+∠D+∠E+∠F=720°,
∴正六边形与六个圆重叠部分的面积为:$\frac{720×π×{1}^{2}}{360}$=2πcm2,
故答案为:2π.
点评 本题考查的是正多边形和圆、相切两圆的性质,掌握多边形的内角和的计算公式、扇形的面积公式是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
16.反比例函数y=$\frac{k}{x}$的图象经过点A(-1,-2),则当x>1时,函数值y的取值范围是( )
| A. | y>1 | B. | 0<y<1 | C. | y>2 | D. | 0<y<2 |
20.“十•一”黄金周期间,我市花果山景区在7天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)旅游开发一方面是给广大市民提供一个休闲游玩的好去处;另一方面是拉动内需,促进消费.若9月30日的游客人数为1万人,进入景区的游客每人平均消费60元,问“十•一”期间所有游客在花果山景区的总消费是多少?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)旅游开发一方面是给广大市民提供一个休闲游玩的好去处;另一方面是拉动内需,促进消费.若9月30日的游客人数为1万人,进入景区的游客每人平均消费60元,问“十•一”期间所有游客在花果山景区的总消费是多少?
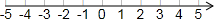 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.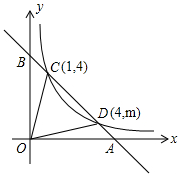 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).