题目内容
用因式分解法解下列方程:
(1)2(x-4)+x(x-4)=0;
(2)4x(5x-3)=3(5x-3);
(3)(3x+2)2-4x2=0;
(4)(t+1)(2t+4)=4;
(5)3(x+4)=x2-16.
(1)2(x-4)+x(x-4)=0;
(2)4x(5x-3)=3(5x-3);
(3)(3x+2)2-4x2=0;
(4)(t+1)(2t+4)=4;
(5)3(x+4)=x2-16.
考点:解一元二次方程-因式分解法
专题:计算题
分析:(1)方程左边分解因式后,利用因式分解法求出解即可;
(2)方程移项变形后,利用因式分解法求出解即可;
(3)方程左边利用平方差公式分解,利用因式分解法求出解即可;
(4)方程整理分解因式,利用因式分解法求出解即可;
(5)方程移项变形分解因式后,利用因式分解法求出解即可.
(2)方程移项变形后,利用因式分解法求出解即可;
(3)方程左边利用平方差公式分解,利用因式分解法求出解即可;
(4)方程整理分解因式,利用因式分解法求出解即可;
(5)方程移项变形分解因式后,利用因式分解法求出解即可.
解答:解:(1)分解因式得:(x+2)(x-4)=0,
可得x+2=0或x-4=0,
解得:x1=-2,x2=4;
(2)方程移项得:4x(5x-3)-3(5x-3)=0,
分解因式得:(4x-3)(5x-3)=0,
解得:x1=
,x2=
;
(3)分解因式得:(3x+2+2x)(3x+2-2x)=0,
解得:x1=-
,x2=-2;
(4)方程整理得:2t2+6t=0,即2t(t+3)=0,
解得:t1=0,t2=-3;
(5)方程变形得:3(x+4)+(x+4)(x-4)=0,
分解因式得:(x+4)(3+x-4)=0,
解得:x1=-4,x2=1.
可得x+2=0或x-4=0,
解得:x1=-2,x2=4;
(2)方程移项得:4x(5x-3)-3(5x-3)=0,
分解因式得:(4x-3)(5x-3)=0,
解得:x1=
| 3 |
| 4 |
| 3 |
| 5 |
(3)分解因式得:(3x+2+2x)(3x+2-2x)=0,
解得:x1=-
| 2 |
| 5 |
(4)方程整理得:2t2+6t=0,即2t(t+3)=0,
解得:t1=0,t2=-3;
(5)方程变形得:3(x+4)+(x+4)(x-4)=0,
分解因式得:(x+4)(3+x-4)=0,
解得:x1=-4,x2=1.
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
把长度为4m的铝线材料按黄金分割切割后,其中较长的一段长度是( )
A、2
| ||
B、2
| ||
C、3-2
| ||
D、6-2
|
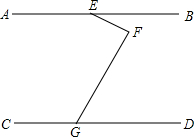 (1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.
(1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由. 如图,已知,点F、C在AD上,且AF=DC,AB∥DE,BC∥EF.求证:△ABC≌△DEF.
如图,已知,点F、C在AD上,且AF=DC,AB∥DE,BC∥EF.求证:△ABC≌△DEF.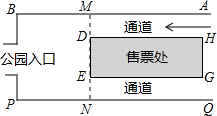 如图,公园入口处前有一间售票处,其屋面DEGH是矩形.售票处后墙DE与两侧通道垂直.小亮的爸爸已购公园门票,在点P处等候小亮,小亮沿售票处北侧的通道中央行进,去找爸爸.
如图,公园入口处前有一间售票处,其屋面DEGH是矩形.售票处后墙DE与两侧通道垂直.小亮的爸爸已购公园门票,在点P处等候小亮,小亮沿售票处北侧的通道中央行进,去找爸爸.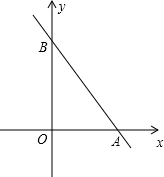 直线y=-
直线y=-