题目内容
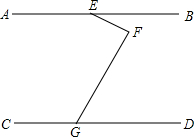 (1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.
(1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.(2)如图AB∥CD,∠AEF=150°,∠DGF=60°.试判断EF和GF的位置关系,并说明理由.
考点:平行线的性质
专题:常规题型
分析:(1)过点F作AB的平行线FH,由平行线的性质可得AB∥FH∥CD,由两直线平行,内错角相等,得到∠BEF=∠EFH,∠FGD=∠HFG,所以∴∠BEF+∠FGD=∠EFH+∠HFG,即∠EFG=∠FGD+∠BEF.
(2)思路同(1)根据∠EFG=∠FGD+∠BEF,求出∠EFG=90°从而得出EF⊥FG.
(2)思路同(1)根据∠EFG=∠FGD+∠BEF,求出∠EFG=90°从而得出EF⊥FG.
解答:(1)解:∠EFG=∠FGD+∠BEF
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等
∴∠BEF+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF
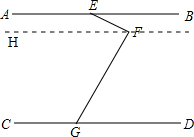
(2)EF⊥FG
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵∠AEF+∠BEF=180°(平角的定义)
∴∠BEF=180°-∠AEF=180°-150°=30°
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等)
∴∠BE+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF=60°+30°=90°
∴EF⊥FG(垂直的定义)

证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等
∴∠BEF+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF

(2)EF⊥FG
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵∠AEF+∠BEF=180°(平角的定义)
∴∠BEF=180°-∠AEF=180°-150°=30°
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等)
∴∠BE+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF=60°+30°=90°
∴EF⊥FG(垂直的定义)

点评:本题主要考查的是平行线的性质:两直线平行,内错角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,O为其内部一点,比较∠BOC和∠A的大小.
如图,在△ABC中,O为其内部一点,比较∠BOC和∠A的大小.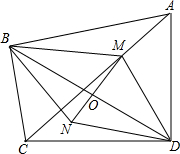 已知:如图所示,四边形ABCD中∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO并延长MO到N,使NO=MO,连接BN与ND.
已知:如图所示,四边形ABCD中∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO并延长MO到N,使NO=MO,连接BN与ND.