如图.小丽从A点出发前进10m.向右转24°.再前进10m.又向右转24°.-.这样一直走下去.他第一次回到出发点A时.一共走了150m．题目和参考答案——青夏教育精英家教网—

题目内容

11．

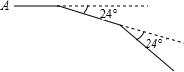如图，小丽从A点出发前进10m，向右转24°，再前进10m，又向右转24°，…，这样一直走下去，他第一次回到出发点A时，一共走了150m．

分析第一次回到出发点A时，所经过的路线正好构成一个外角是24度的正多边形，求得边数，即可求解．

解答解：360÷24=15，
则一共走了15×10=150m．
故答案为：150．

点评本题考查了正多边形的外角的计算，第一次回到出发点A时，所经过的路线正好构成一个外角是15度的正多边形是关键．

练习册系列答案

学习总动员期末加暑假光明日报出版社系列答案

相关题目

1．先化简，再求值：（a-1）²+a（a+2），其中a=$\sqrt{5}$．

2．求下列各式中x的值
（1）4x²-16=0
（2）$\frac{1}{3}{x^3}-9=0$．

19．观察下列等式：$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1，$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$，$\frac{1}{\sqrt{4}-\sqrt{3}}$=$\sqrt{4}$-$\sqrt{3}$…
请从上边找到规律，计算$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$=$\sqrt{2013}$-1．

6．若（x+2012）²=987654321，则（x+2022）（x+2002）的值是（　　）

16．已知x+y=7，xy=2，求2x²+2y²；（x-y）²．

3．

花果山水果超市以3元/kg的价格购进一批水蜜桃，并对其进行筛选分为甲级水蜜挑与乙级水蜜挑后开始销售．阅读下面的情景对恬．回答问题．
（1）分别求甲级水蜜桃与乙级水蜜桃的单价．
（2）销售结束后，店长统计发现：甲乙两级水蜜桃每天都有销量，甲级水蜜桃从开始销售至销售的第x天的总销量y_甲（kg）与x的关系为y_甲=-x²+50x；乙级水蜜桃从开始销售至销售第x天的总销量y_乙（kg）与x的关系为y_乙=3x²+10x
①问是否存在至某一天甲级水蜜桃与乙级水蜜桃的总销量相等，若存在，求至这一天销售水蜜桃已获得毛利润；若不存在，请说明理由
②问从第几天起，乙级水蜜桃每天的销量比甲级水蜜桃的销量至少多4kg？

20．若a²+ab+b²+A=（a+b）²，那么A等于（　　）

1．

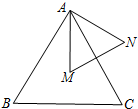如图，△ABC和△AMN都是等边三角形，点M是△ABC的重心，那么$\frac{{S}_{△AMN}}{{S}_{△ABC}}$的值为（　　）

试题分类