题目内容
18. 如图所示,在矩形ABCD中,对角线AC,BD相交于点O.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O.(1)过点O作0E⊥BC于点E,连接DE交OC于点F,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出位似比;若不是,请说明理由.
(2)连接DG交AC于点H,作HI⊥BC于I,试确定$\frac{CI}{BC}$的值.
分析 (1)根据相似三角形的判定定理证明△ABC∽△FGC,根据位似变换的概念和位似中心的概念解答即可,根据相似三角形的性质求出两个三角形的相似比,得到位似比;
(2)根据相似三角形的性质进行计算即可.
解答 解:(1)∵FG⊥BC,AB⊥BC,
∴FG∥AB,
∴△ABC∽△FGC,
△ABC与△FGC对应顶点的连线相交于一点,对应边互相平行或重合,
∴△ABC与△FGC是位似图形,位似中心是点C,
∵BO=OD,OE∥CD,
∴$\frac{DC}{OE}$=$\frac{BD}{OB}$=2
∴$\frac{CF}{FO}$=$\frac{DC}{OE}$=2,
∴$\frac{CG}{CE}$=$\frac{2}{3}$,
∴$\frac{CG}{CB}$=$\frac{1}{3}$,
则△ABC与△FGC的位似比为3;
(2)由(1)得,$\frac{EG}{EC}$=$\frac{1}{3}$,FG∥CD,
∴$\frac{FG}{CD}$=$\frac{EG}{EC}$=$\frac{1}{3}$,
∴$\frac{CI}{CG}$=$\frac{CH}{CF}$=$\frac{3}{4}$,又$\frac{CG}{CE}$=$\frac{2}{3}$,
∴$\frac{CI}{CE}$=$\frac{1}{2}$,
∴$\frac{CI}{BC}$=$\frac{1}{4}$.
点评 本题考查的是位似变换的概念、位似比的计算,相似三角形的判定和性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了20次测试,测试成绩如下表(单位:环):
(1)根据表格中的数据,分别计算出甲、乙两人的平均成绩;
(2)你认为推荐谁参加省比赛更合适,请说明理由.
| 成绩(环) | 7 | 8 | 9 | 10 |
| 甲 | 3次 | 8次 | 5次 | 4次 |
| 乙 | 4次 | 6次 | 6次 | 4次 |
(2)你认为推荐谁参加省比赛更合适,请说明理由.
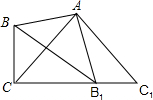 如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上. 如图所示,已知AD是Rt△ABC的斜边BC上的高,E为AC上一点,连接BE交AD于点F,若AE=AF,求证:BE平分∠ABC.
如图所示,已知AD是Rt△ABC的斜边BC上的高,E为AC上一点,连接BE交AD于点F,若AE=AF,求证:BE平分∠ABC. 如图,直线y=kx+2与直线y=$\frac{1}{3}$x相交于点A(3,1),与x轴交于点B.
如图,直线y=kx+2与直线y=$\frac{1}{3}$x相交于点A(3,1),与x轴交于点B. 如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.