题目内容
11.已知直线y=kx+b经过M(0,3),N(4,-1)两点,则不等式-1<kx+b≤3的解集为0≤x<4.分析 首先根据直线经过的两点的坐标求得函数的解析式,然后解不等式即可.
解答 解:∵直线y=kx+b经过M(0,3),N(4,-1)两点,
$\left\{\begin{array}{l}{b=3}\\{4k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴不等式为-1<-x+3≤3,
解得:0≤x<4,
故答案为:0≤x<4.
点评 本题考查了一次函数与一元一次不等式的知识,解题的关键是能够根据点的坐标求得解析式,从而得到不等式,难度不大.

练习册系列答案
相关题目
19.某地的国际标准时间(GMT)是指该地与格林尼治(Greenwich)的时差.以下为同一时刻5个城市的国际标准时间(正数表示当地时间比格林尼治时间早的时数,负数表示当地时间比格林尼治时间迟的时数)
(1)伦敦时间中午12点时,京和多伦多的当地间分别是几点?
(2)北京时间早晨7点时,纽约的当地时间是几点?
| 城市 | 伦敦 | 北京 | 东京 | 多伦多 | 纽约 |
| 国际标准时间 | 0 | +8 | +9 | -4 | -5 |
(2)北京时间早晨7点时,纽约的当地时间是几点?
6.下列多项式能分解因式的是( )
| A. | x2-y | B. | x2+1 | C. | x2+xy+y2 | D. | x2-4xy+4y2 |
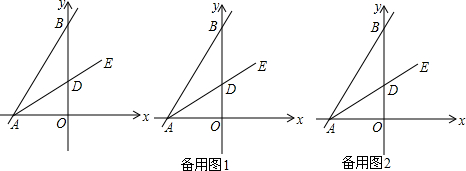
 如图,等边△ABC的边长为4,点E在BA的延长线上,点D在BC边上,且ED=EC,AE=2.求BD的长.
如图,等边△ABC的边长为4,点E在BA的延长线上,点D在BC边上,且ED=EC,AE=2.求BD的长.