题目内容
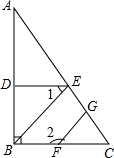 如图,已知DE⊥AB,BC⊥AB,∠1+∠2=180°,判断BE与FG是否平行,并说明理由.
如图,已知DE⊥AB,BC⊥AB,∠1+∠2=180°,判断BE与FG是否平行,并说明理由.考点:平行线的判定与性质
专题:
分析:根据平行线的判定推出DE∥BC,根据平行线的性质推出∠1=∠EBF,求出∠2+∠EBF=180°,根据平行线的判定推出即可.
解答:解:BE∥FG,
理由是:∵DE⊥AB,BC⊥AB,
∴∠ADE=∠ABC=90°,
∴DE∥BC,
∴∠1=∠EBF,
∵∠1+∠2=180°,
∴∠2+∠EBF=180°,
∴BE∥FG.
理由是:∵DE⊥AB,BC⊥AB,
∴∠ADE=∠ABC=90°,
∴DE∥BC,
∴∠1=∠EBF,
∵∠1+∠2=180°,
∴∠2+∠EBF=180°,
∴BE∥FG.
点评:本题考查了平行线的性质和判定的应用,主要考查学生运用定理进行推理的能力,难度适中.

练习册系列答案
相关题目
直线y=2x与直线y=2x+1的位置关系为( )
| A、垂直 | B、重合 |
| C、平行 | D、以上都有可能 |
不等式5>
≥-1的最大整数解为( )
| x-3 |
| 2 |
| A、11 | B、12 | C、13 | D、14 |

 如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.
如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6. 如图,A、B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、C、A在同一直线上,则DE的长就是A、B之间的距离,请你说明道理,你还能想出其他方法吗?
如图,A、B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、C、A在同一直线上,则DE的长就是A、B之间的距离,请你说明道理,你还能想出其他方法吗?