题目内容
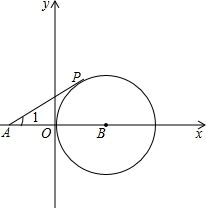 如图,⊙O切y轴于原点O,过点A(-2
如图,⊙O切y轴于原点O,过点A(-2| 3 |
(1)求⊙B的半径r及直线AP的解析式;
(2)是否存在点N(0,b),使△APN是直角三角形?若存在,求b的值;若不存在,请说明理由.
考点:圆的综合题
专题:综合题
分析:(1)连结BP,作PH⊥AB于H,如图,根据切线的性质得到∠APB=90°,OB=r,在Rt△ABP中利用含30度的直角三角形三边的关系2
+r=2r,即可解得r=2
;再在Rt△PBH中计算出BH=
PB=
,PH=
BH=3,则P点坐标为(
,3),然后利用待定系数法求直线AP的解析式;
(2)先根据两点间的距离公式得到AN2=(2
)2+b2,AP2=(
+2
)2+32=36,PN2=(
)2+(b-3)2,然后分类讨论:当∠APN=90°时,AP2+PN2=AN2,即36+(
)2+(b-3)2=(2
)2+b2,;当∠PAN=90°时,AP2+PN2=AN2,即36+(2
)2+b2=(
)2+(b-3)2;当∠ANP=90°时,AN2+PN2=AP2,即(2
)2+b2+(
)2+(b-3)2=36,再分别解关于b的方程即可.
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
(2)先根据两点间的距离公式得到AN2=(2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:(1)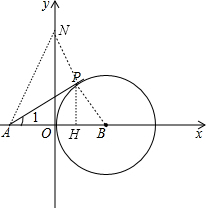 连结BP,作PH⊥AB于H,如图,
连结BP,作PH⊥AB于H,如图,
∵AP切⊙B于P,
∴PB⊥AP,
∴∠APB=90°,
∵⊙O切y轴于原点O,
∴OB=r,
在Rt△ABP中,PB=OB=r,
∵∠1=30°,
∴AB=2PB,
∴2
+r=2r,
∴r=2
;
在Rt△PBH中,∵∠PBH=60°,PB=2
,
∴BH=
PB=
,PH=
BH=3,
∴OH=OB-BH=
,
∴P点坐标为(
,3),
设直线AP的解析式为y=kx+b,
把A(-2
,0),P(
,3)代入得
,解得
,
∴直线AP的解析式为y=
x+2;
(2)存在.
∵A(-2
,0),N(0,b),P(
,3),
∴AN2=(2
)2+b2,AP2=(
+2
)2+32=36,PN2=(
)2+(b-3)2,
当∠APN=90°时,AP2+PN2=AN2,即36+(
)2+(b-3)2=(2
)2+b2,解得b=6;
当∠PAN=90°时,AP2+PN2=AN2,即36+(2
)2+b2=(
)2+(b-3)2,解得b=-6;
当∠ANP=90°时,AN2+PN2=AP2,即(2
)2+b2+(
)2+(b-3)2=36,整理得b2-3b-4=0,解得b1=4,b2=-1,
综上所述,b的值为-6或-1或4或6.
 连结BP,作PH⊥AB于H,如图,
连结BP,作PH⊥AB于H,如图,∵AP切⊙B于P,
∴PB⊥AP,
∴∠APB=90°,
∵⊙O切y轴于原点O,
∴OB=r,
在Rt△ABP中,PB=OB=r,
∵∠1=30°,
∴AB=2PB,
∴2
| 3 |
∴r=2
| 3 |
在Rt△PBH中,∵∠PBH=60°,PB=2
| 3 |
∴BH=
| 1 |
| 2 |
| 3 |
| 3 |
∴OH=OB-BH=
| 3 |
∴P点坐标为(
| 3 |
设直线AP的解析式为y=kx+b,
把A(-2
| 3 |
| 3 |
|
|
∴直线AP的解析式为y=
| ||
| 3 |
(2)存在.
∵A(-2
| 3 |
| 3 |
∴AN2=(2
| 3 |
| 3 |
| 3 |
| 3 |
当∠APN=90°时,AP2+PN2=AN2,即36+(
| 3 |
| 3 |
当∠PAN=90°时,AP2+PN2=AN2,即36+(2
| 3 |
| 3 |
当∠ANP=90°时,AN2+PN2=AP2,即(2
| 3 |
| 3 |
综上所述,b的值为-6或-1或4或6.
点评:本题考查了圆的综合题:熟练掌握切线的性质;会运用待定系数法求一次函数的解析式;会运用勾股定理、两点间的距离公式和含30度的直角三角形三边的关系进行几何计算;理解坐标与图形性质;能运用分类讨论的思想解决数学问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )
如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )| A、60° | B、70° |
| C、80° | D、140° |
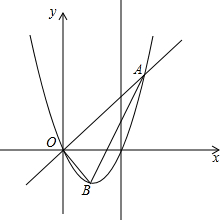 如图,已知直线y=x与二次函数y=x2+bx的图象交于点A、O,(O是坐标原点),点B为二次函数图象的顶点,OA=3
如图,已知直线y=x与二次函数y=x2+bx的图象交于点A、O,(O是坐标原点),点B为二次函数图象的顶点,OA=3