题目内容
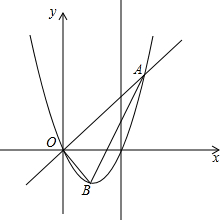 如图,已知直线y=x与二次函数y=x2+bx的图象交于点A、O,(O是坐标原点),点B为二次函数图象的顶点,OA=3
如图,已知直线y=x与二次函数y=x2+bx的图象交于点A、O,(O是坐标原点),点B为二次函数图象的顶点,OA=3| 2 |
(1)求b的值及过B、A两点的一次函数的解析式;
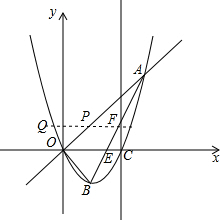
(2)抛物线的对称轴与x轴交于C,点P在线段OA上,Q在抛物线上,且PQ∥x轴,若以O、C、P、Q为顶点的四边形是平行四边形时,求点Q的坐标;
(3)若点P在线段OA上,Q在抛物线上,且PQ∥x轴,PQ将△AOB的面积二等分时,求点P的坐标.
考点:二次函数综合题
专题:
分析:(1)由点A在直线y=x上,可知A的横纵坐标相等,又因为OA=3
,所以可以求出A的坐标,再把A的坐标代入y=x2+bx,求出b的值即可求出函数的解析式;
(2)用配方法求出顶点P的坐标,设Q的坐标为(x,x2-2x),则P(x2-2x,x2-2x),根据平行四边形的性质即可求得结论;
(3)先求得三角形AOB的面积为
,然后根据题意求得S△APF=
,根据相似三角形的性质得到比例式,得出△APF底边PF上的高h,即可求得P的纵坐标,进而求得P的坐标.
| 2 |
(2)用配方法求出顶点P的坐标,设Q的坐标为(x,x2-2x),则P(x2-2x,x2-2x),根据平行四边形的性质即可求得结论;
(3)先求得三角形AOB的面积为
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:(1)∵点A在直线y=x上,且OA=3
,
∴A点的坐标是(3,3)
∵点A(3,3)在函数y=x2+bx的图象上,
∴3=9+3b,
解得:b=-2,
故二次函数的解析式是y=x2-2x;
(2)∵y=x2-2x=(x-1)2-1,
∴顶点B的坐标为(1,-1)
设Q的坐标为(x,x2-2x),则P(x2-2x,x2-2x),
∵以O、C、P、Q为顶点的四边形是平行四边形时,
∴PQ=OC=1,
∴x2-2x-x=1,即x2-3x-1=0,解得,x=
或x=
,
∴Q(
,
)或(
,
);
 (3)A(3,3),B(1,-1),
(3)A(3,3),B(1,-1),
∴直线AB的解析式为y=2x-3,
∴直线AB与x轴的交点E为(
,0),
S△OEB=
×
×1=
,S△AOE=
×
×3=
,
∴S△AOB=S△OEB+S△AOE=
+
=3,
∵PQ将△AOB的面积二等分,
∴S△APF=
,
∵PQ∥x轴,
∴△APF∽△AOE,
∴(
)2=
=
=
,
∴h=
,
∴P点的纵坐标为3-
,
∵P在线段OA上,
∴P(3-
,3-
).
| 2 |
∴A点的坐标是(3,3)
∵点A(3,3)在函数y=x2+bx的图象上,
∴3=9+3b,
解得:b=-2,
故二次函数的解析式是y=x2-2x;
(2)∵y=x2-2x=(x-1)2-1,
∴顶点B的坐标为(1,-1)
设Q的坐标为(x,x2-2x),则P(x2-2x,x2-2x),
∵以O、C、P、Q为顶点的四边形是平行四边形时,
∴PQ=OC=1,
∴x2-2x-x=1,即x2-3x-1=0,解得,x=
3+
| ||
| 2 |
3-
| ||
| 2 |
∴Q(
3+
| ||
| 2 |
5+
| ||
| 2 |
3-
| ||
| 2 |
5-
| ||
| 2 |
 (3)A(3,3),B(1,-1),
(3)A(3,3),B(1,-1),∴直线AB的解析式为y=2x-3,
∴直线AB与x轴的交点E为(
| 3 |
| 2 |
S△OEB=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
∴S△AOB=S△OEB+S△AOE=
| 3 |
| 4 |
| 9 |
| 4 |
∵PQ将△AOB的面积二等分,
∴S△APF=
| 3 |
| 2 |
∵PQ∥x轴,
∴△APF∽△AOE,
∴(
| h |
| 3 |
| S△APF |
| S△AOE |
| ||
|
| 2 |
| 3 |
∴h=
| 6 |
∴P点的纵坐标为3-
| 6 |
∵P在线段OA上,
∴P(3-
| 6 |
| 6 |
点评:本题考查了用待定系数法求二次函数的解析式、二次函数的顶点坐标、平行四边形的性质,相似三角形的判定和性质,解题时也要注意分类讨论数学思想的运用,题目的综合性很强,难度中等.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
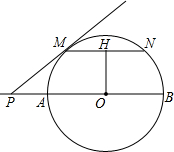 如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求:
如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求: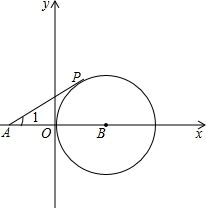 如图,⊙O切y轴于原点O,过点A(-2
如图,⊙O切y轴于原点O,过点A(-2