题目内容
3.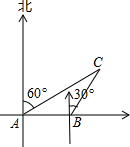 如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.
如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.
分析 过点C作CM⊥AB于M,设CM=x,根据题意和特殊角的三角函数值求出AM和BM的值,从而求出x的值,即可得到结论.
解答  解:过点C作CM⊥AB于M,设CM=x,
解:过点C作CM⊥AB于M,设CM=x,
∵∠CAM=30°,∠CBM=60°,
∴AM=$\sqrt{3}$x,BC=$\frac{2\sqrt{3}}{3}$x,BM=$\frac{\sqrt{3}}{3}$x,
由题意知:AM-BM=$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=20,
∴x=10$\sqrt{3}$,
∴AC=20$\sqrt{3}$,BC=20,
∴甲船的速度=$\frac{20\sqrt{3}}{\frac{1}{2}}$=40$\sqrt{3}$海里/小时,乙船的速度=$\frac{20}{\frac{1}{2}}$=40海里/小时.
点评 此题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、方向角问题,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
相关题目
12. 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )
 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
9.某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是( )
| A. | $\frac{240}{x-20}$-$\frac{120}{x}$=4 | B. | $\frac{240}{x+20}$-$\frac{120}{x}$=4 | C. | $\frac{120}{x}$-$\frac{240}{x-20}$=4 | D. | $\frac{120}{x}$-$\frac{240}{x+20}$=4 |
15.下列叙述正确的是( )
①三角形的中线、角平分线都是射线
②三角形的三条高线交于一点
③三角形的中线就是经过一边中点的线段
④三角形的三条角平分线交于一点
⑤三角形的中线将三角形分成面积相等的两个小三角形.
①三角形的中线、角平分线都是射线
②三角形的三条高线交于一点
③三角形的中线就是经过一边中点的线段
④三角形的三条角平分线交于一点
⑤三角形的中线将三角形分成面积相等的两个小三角形.
| A. | ④⑤ | B. | ①②④ | C. | ②④ | D. | ④ |
 如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.
如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.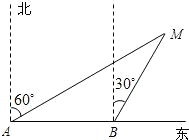 如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?
如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?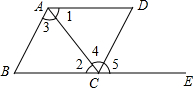 如图,下列能判定AB∥CD的条件有( )个.
如图,下列能判定AB∥CD的条件有( )个. 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC