题目内容
12.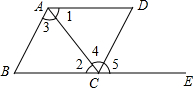 如图,下列能判定AB∥CD的条件有( )个.
如图,下列能判定AB∥CD的条件有( )个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;
(4)∠B=∠5;(5)∠B+∠BAD=180°; (6)∠B=∠D.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答 解:(1)利用同旁内角互补判定两直线平行,故(1)正确;
(2)利用内错角相等判定两直线平行,∵∠1=∠2,∴AD∥BC,而不能判定AB∥CD,故(2)错误;
(3)利用内错角相等判定两直线平行,故(3)正确;
(4)利用同位角相等判定两直线平行,故(4)正确.
(5)利用同旁内角互补两直线平行,根据∠B+∠BAD=180°,可证得BC∥AD,不能得到AB∥CD,故(5)错误;
(6)∠B和∠D不是同位角,也不是内错角,无法判断AB∥CD,故(6)错误.
∴正确的为(1)、(3)、(4),共3个;
点评 本题考查了平行线的判定方法,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两直线平行.

练习册系列答案
相关题目
20.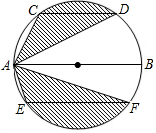 运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
 运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )| A. | $\frac{25}{2}$π | B. | 10π | C. | 24+4π | D. | 24+5π |
20. 一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )
一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )
 一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )
一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=( )| A. | 70° | B. | 90° | C. | 110° | D. | 180° |
7.已知关于x的不等式组 $\left\{\begin{array}{l}{x-a≥0}\\{3-2x≥-1}\end{array}\right.$无解,则a的取值范围是( )
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
17.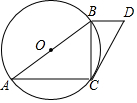 如图,在⊙O中,AB是直径,点C在圆上,∠A=30°,BD∥AC,且BD=$\frac{1}{3}$AC.
如图,在⊙O中,AB是直径,点C在圆上,∠A=30°,BD∥AC,且BD=$\frac{1}{3}$AC.
(1)求∠D的度数;
(2)求证:DC是⊙O的切线;
(3)连接AD,求tan∠BAD的值.
 如图,在⊙O中,AB是直径,点C在圆上,∠A=30°,BD∥AC,且BD=$\frac{1}{3}$AC.
如图,在⊙O中,AB是直径,点C在圆上,∠A=30°,BD∥AC,且BD=$\frac{1}{3}$AC.(1)求∠D的度数;
(2)求证:DC是⊙O的切线;
(3)连接AD,求tan∠BAD的值.
1. 下面几何体的左视图是( )
下面几何体的左视图是( )
 下面几何体的左视图是( )
下面几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
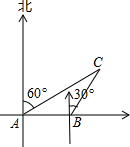 如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.
如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.