题目内容
16.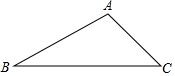 如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.
如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
分析 (1)如图作AD⊥BC于D.则AD=10m,求出CD、BD即可解决问题.
(2)求出汽车的速度,即可解决问题,注意统一单位;
解答 解:(1)如图作AD⊥BC于D.则AD=10m,
在Rt△ACD中,∵∠C=45°,
∴AD=CD=10m,
在Rt△ABD中,∵∠B=30°,
∴tan30°=$\frac{AD}{BD}$,
∴BD=$\sqrt{3}$AD=10$\sqrt{3}$m,
∴BC=BD+DC=(10+10$\sqrt{3}$)m.
(2)结论:这辆汽车超速.
理由:∵BC=10+10$\sqrt{3≈}$27m,
∴汽车速度=$\frac{27}{0.9}$=30m/s=108km/h,
∵108>80,
∴这辆汽车超速.
点评 本题考查解直角三角形的应用,锐角三角函数、速度、时间、路程之间的关系等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
6.下列事件为必然事件的是( )
| A. | 五边形的外角和是360° | B. | 打开电视机,它正在播广告 | ||
| C. | 明天太阳从西方升起 | D. | 抛掷一枚硬币,一定正面朝上 |
4.2016年,我市“全面改薄”和解决大班额工程成绩突出,两项工程累计开工面积达477万平方米,各项指标均居全省前列.477万用科学记数法表示正确的是( )
| A. | 4.77×105 | B. | 47.7×105 | C. | 4.77×106 | D. | 0.477×106 |
10. 如图,一条直线AB上有一点O,∠AOM=90°,∠COD=90°,∠COD在平角∠AOB内左右摆动(O点不动,OC与OA、OD与OB均不重合),在摆动时,除直角外,保持相等的角有( )
如图,一条直线AB上有一点O,∠AOM=90°,∠COD=90°,∠COD在平角∠AOB内左右摆动(O点不动,OC与OA、OD与OB均不重合),在摆动时,除直角外,保持相等的角有( )
 如图,一条直线AB上有一点O,∠AOM=90°,∠COD=90°,∠COD在平角∠AOB内左右摆动(O点不动,OC与OA、OD与OB均不重合),在摆动时,除直角外,保持相等的角有( )
如图,一条直线AB上有一点O,∠AOM=90°,∠COD=90°,∠COD在平角∠AOB内左右摆动(O点不动,OC与OA、OD与OB均不重合),在摆动时,除直角外,保持相等的角有( )| A. | 一对 | B. | 两对 | C. | 三对 | D. | 四对 |
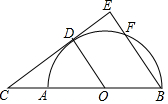 如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.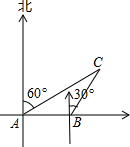 如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.
如图,B在A的正东方向20海里处,甲船从A处出发,沿北偏东60°方向行驶,乙船从B处出发,沿北偏东30°方向行驶.若甲、乙两船同时出发,半小时后又同时到达C处,求两船的速度.