题目内容
如图，AB为⊙O的直径，AB=10cm，动弦CD=6cm，动弦CD始终与AB相交，问当CD弦在⊙O上滑动时，A、B到直线CD距离之差的绝对值是否发生变化？若变化，请说明理由；若不变，予以证明并求其值．考点：相似三角形的判定与性质,垂径定理
专题：
分析：设AB与CD交于H，作OM⊥CD于M，AF⊥CD于F，易得OM，MC，MD的长度，再由△AFH∽△OMH∽△BEH，得出比例式，化简两式相减求解即可．
解答：解：如图，设AB与CD交于H，作OM⊥CD于M，AF⊥CD于F，
∵CD=6cm，
∴MC=MD=3，
∵AB=10cm，
∴OM=4，
∵△AFH∽△OMH∽△BEH，
∴
=
=
，
∴
=
，①
∴
=
=
，即
=
，②
①-②得到
=-2，
∴|AF-BE|=2，
∴当CD弦在⊙O上滑动时，A、B到直线CD距离之差的绝对值不发生变化．
∵CD=6cm，
∴MC=MD=3，
∵AB=10cm，
∴OM=4，
∵△AFH∽△OMH∽△BEH，
∴
| AF |
| OM |
| AH |
| HO |
| 5-OH |
| OH |
∴
| AF |
| 4 |
| 5-OH |
| OH |
∴
| EB |
| OM |
| HB |
| OH |
| 5+OH |
| OH |
| BE |
| 4 |
| 5+OH |
| OH |
①-②得到
| AF-BE |
| 4 |
∴|AF-BE|=2，
∴当CD弦在⊙O上滑动时，A、B到直线CD距离之差的绝对值不发生变化．
点评：本题主要考查了相似三角形的判定与性质及垂径定理，解题的关键是正确作出辅助线，利用三角形相似列出比例式求解．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
已知a1，a2，…，a2004都是正数，如果M=（a1+a2+…+a2003）（a2+a3+…+a2004），N=（a1+a2+…+a2004）（a2+a3+…+a2003），那么M、N的大小关系是（ ）
| A、M＞N | B、M＜N |
| C、M=N | D、不确定的 |
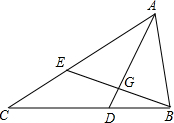在△ABC中，AB＜BC＜CA，且AC-AB=2，D点在边BC上，且AD平分∠BAC．E为边AC上的一点，连接BE交AD于点G，且
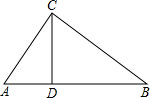如图所示，已知△ABC中，∠C=90°，CD⊥AB，垂足为D，已知AC=3，BC=4． 
已知六边形ABCDEF的每个角都相等，MN⊥DE，求证：MN⊥AB．