题目内容
16. 如图,⊙M交x轴于A(-1,0),B(3,0)两点.交y轴于C(0,-3),D(0,1)两点.
如图,⊙M交x轴于A(-1,0),B(3,0)两点.交y轴于C(0,-3),D(0,1)两点.(1)求点M的坐标;
(2)求弧BD的长.
分析 (1)过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,由垂径定理得出EB=$\frac{1}{2}$AB=2,得出OE=1,同理可得OF=1,证四边形OEMF为正方形,得出EM=EF=1,即可得出结果;
(2)连接MD,BC,由勾股定理可得BM=$\sqrt{5}$,证出∠BCO=45°,得出∠BMD=90°,由弧长公式即可得出结果.
解答 解:(1)如图1所示,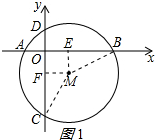 过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,
过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,
则EB=$\frac{1}{2}$AB=2,四边形OENF是矩形,
∴OE=1,
同理可得OF=1,
∴OEOF,
∴四边形OEMF为正方形,
∴EM=EF=1,
∴M(1,-1);
(2)连接MD,BC,如图2所示: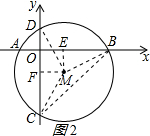
由勾股定理可得BM=$\sqrt{5}$,
∵∠BOC=90°,OB=OC,
∴∠BCO=45°,
∴∠BMD=90°,
∴弧BD的长=$\frac{90π×\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π.
点评 本题考查了垂径定理、坐标与图形性质、勾股定理、正方形的判定与性质、圆周角定理、弧长公式等知识;熟练掌握垂径定理,由圆周角定理求出∠BMD是解决问题(2)的关键.

练习册系列答案
相关题目
7.将分式$\frac{2xy}{x-y}$中x,y都扩大3倍,那么分式的值( )
| A. | 变为原来的3倍 | B. | 变为原来的6倍 | C. | 变为原来的9倍 | D. | 不变 |
4.下列运算中,正确的是( )
| A. | a•a2=a3 | B. | (3a)2=3a2 | C. | 3a6÷a3=3a2 | D. | (ab2)2=a2b2 |
11.下列函数中,y随x的增大而减小的是( )
| A. | y=1+2x | B. | y=$\frac{2}{x}(x≥0)$ | C. | y=-$\frac{1}{x}$ | D. | y=x2(x≥0) |
5. 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;
(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论: