题目内容
10. 如图,将三角形纸片ABC沿BD折叠,点A摞在边BC上的点E处,将纸片沿DE折叠,点C恰好落在点B处.
如图,将三角形纸片ABC沿BD折叠,点A摞在边BC上的点E处,将纸片沿DE折叠,点C恰好落在点B处.(1)写出图中所有相等的线段;
(2)求证:DE⊥BC;
(3)求∠C的度数.
分析 (1)根据翻折变换前后的对应线段相等解答;
(2)根据翻折前后的对应角相等可得∠BED=∠CED,再根据平角等于180°求出∠BED=90°,然后根据垂直的定义证明;
(3)根据翻折变换的性质求出∠A=90°,∠ABD=∠CBD,再根据直角三角形两锐角互余列方程求解即可.
解答 (1)解:∵三角形纸片ABC沿BD折叠,点A落在边BC上的点E处,
∴AB=BE,AD=DE,
∵纸片沿DE折叠,点C恰好落在点B处,
∴CD=BD,BE=CE,
∴相等的线段有AB=BE=CE,BD=CD,AD=DE;
(2)证明:∵纸片沿DE折叠,点C恰好落在点B处,
∴∠BED=∠CED,
又∵∠BED+∠CED=180°,
∴∠BED=90°,
∴DE⊥BC;
(3)∵三角形纸片ABC沿BD折叠,点A落在边BC上的点E处,
∴∠A=∠BED=90°,∠ABD=∠CBD,
∵纸片沿DE折叠,点C恰好落在点B处,
∴∠C=∠CBD,
在△ABC中,∠C+∠ABD+∠CBD=3∠C=90°,
∴∠C=30°.
点评 本题考查了翻折变换的性质,直角三角形两锐角互余的性质,翻折变换前后对应线段相等,对应角相等.

练习册系列答案
相关题目
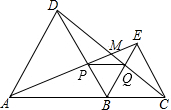 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M、P,CD交BE于点Q,连接PQ,BM.下列结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC.其中结论正确的是①②③④.
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M、P,CD交BE于点Q,连接PQ,BM.下列结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC.其中结论正确的是①②③④. 如图,点B,C,D在同一条直线上,△ABC和△ECD都是等边三角形,△EBC可以看作是△DAC绕点C逆时针旋转60°得到.
如图,点B,C,D在同一条直线上,△ABC和△ECD都是等边三角形,△EBC可以看作是△DAC绕点C逆时针旋转60°得到. 如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.
如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.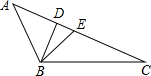 喜羊羊、美羊羊、懒羊羊在微信建立了一个学习讨论组,现在他们讨论了一道几何题,如图所示,请你填写完整的解答过程.
喜羊羊、美羊羊、懒羊羊在微信建立了一个学习讨论组,现在他们讨论了一道几何题,如图所示,请你填写完整的解答过程.