题目内容
3.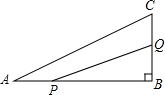 如图,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,多少时间后P、Q之间的距离等于4$\sqrt{2}$cm?
如图,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,多少时间后P、Q之间的距离等于4$\sqrt{2}$cm?
分析 设经过x秒,P、Q之间的距离等于4$\sqrt{2}$cm.先用含x的代数式分别表示BP和BQ的长度,进一步利用勾股定理建立方程求得答案即可.
解答 解:设点P、Q分别从点A、B同时出发,xs后P、Q之间的距离等于4$\sqrt{2}$cm,
∵AP=1•x=x,BQ=2x,
∴BP=AB-AP=6-x,
∴BP2+BQ2=PQ2,
即(6-x)2+(2x)2=(4$\sqrt{2}$)2,
解得:x1=$\frac{2}{5}$,x2=2(不合题意,舍去).
答:点P、Q分别从点A、B同时出发,$\frac{2}{5}$s后P、Q之间的距离等于4$\sqrt{2}$cm.
点评 本题考查了一元二次方程的应用.关键是用含时间的代数式准确表示BP和BQ的长度,再根据勾股定理列出一元二次方程,进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 如图,函数y=3x与y=kx+b的图象交于点A(2,6),则不等式3x<kx+b的解集为( )
如图,函数y=3x与y=kx+b的图象交于点A(2,6),则不等式3x<kx+b的解集为( )
 如图,函数y=3x与y=kx+b的图象交于点A(2,6),则不等式3x<kx+b的解集为( )
如图,函数y=3x与y=kx+b的图象交于点A(2,6),则不等式3x<kx+b的解集为( )| A. | x<4 | B. | x<2 | C. | x>2 | D. | x>4 |
15.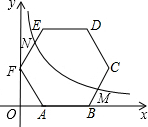 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )| A. | ($\frac{7}{4}\sqrt{3},4$) | B. | ($\frac{7}{4},4\sqrt{3}$) | C. | (2$\sqrt{2}-1,2\sqrt{6}+\sqrt{3}$) | D. | (2$\sqrt{2}+1,2\sqrt{6}-\sqrt{3}$) |
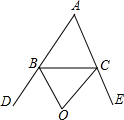 如图,OB、OC是△ABC的外角平分线,若∠A=50°,求∠BOC的度数.
如图,OB、OC是△ABC的外角平分线,若∠A=50°,求∠BOC的度数. 如图,E、F分别是AB、CD上一点,∠2=∠D,∠1与∠C互余,BC⊥AB,试说明AB∥CD.
如图,E、F分别是AB、CD上一点,∠2=∠D,∠1与∠C互余,BC⊥AB,试说明AB∥CD.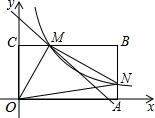 如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.