题目内容
6.(1)如图,?ABCD中,E、F、G、H为各边中点,请用三种不同的方法,通过适当连线,找出?ABCD的对称中心P.(2)圆内接正五边形是否中心对称图形否(填“是”或“否”)

分析 (1)首先确定出图形中的对应点,然后连接对应点,找出交点即可;
(2)根据中心对称图形的概念和各图形的特点即可解答.
解答 解:(1)如图所示:
(2)正五边形是奇数边形,绕中心旋转180度后所得的图形与原图形不会重合.
故答案为:否.
点评 此题主要考查了中心对称图形的概念.找出对称点是解题的本题的关键,任意两组对称点连线的交点即为对称中心.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11.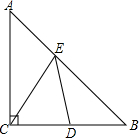 如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
 如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
15.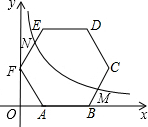 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )| A. | ($\frac{7}{4}\sqrt{3},4$) | B. | ($\frac{7}{4},4\sqrt{3}$) | C. | (2$\sqrt{2}-1,2\sqrt{6}+\sqrt{3}$) | D. | (2$\sqrt{2}+1,2\sqrt{6}-\sqrt{3}$) |
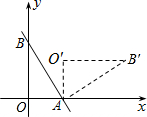 如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是(3,1).
如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是(3,1).
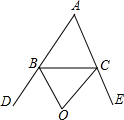 如图,OB、OC是△ABC的外角平分线,若∠A=50°,求∠BOC的度数.
如图,OB、OC是△ABC的外角平分线,若∠A=50°,求∠BOC的度数.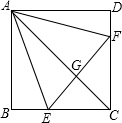 如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论:
如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论: