题目内容
在Rt△ABC中,∠ABC=90°,OC为中线,AC=6,OC为中线,AC=6,OC=5,求:AB,BC的长及△ABC的面积.
考点:勾股定理
专题:
分析:过点O作OD⊥AB交AC于D,求出AD=CD,OD=
BC,然后在Rt△AOD和Rt△BOC中利用勾股定理列出方程,求解即可,再利用三角形的面积公式列式计算即可得解.
| 1 |
| 2 |
解答: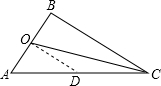 解:如图,过点O作OD⊥AB交AC于D,
解:如图,过点O作OD⊥AB交AC于D,
∵∠ABC=90°,OC为中线,
∴AD=CD=
AC=3,OD=
BC,
在Rt△AOD中,AO2+OD2=AD2=9,
在Rt△BOC中,OB2+BC2=OC2=25,
∵OC为中线,
∴AO=OB,
∴BC2-OD2=16,
∴
BC2=16,
解得BC=
,
AB=
=
=
,
S△ABC=
BC•AB=
×
×
=
.
 解:如图,过点O作OD⊥AB交AC于D,
解:如图,过点O作OD⊥AB交AC于D,∵∠ABC=90°,OC为中线,
∴AD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOD中,AO2+OD2=AD2=9,
在Rt△BOC中,OB2+BC2=OC2=25,
∵OC为中线,
∴AO=OB,
∴BC2-OD2=16,
∴
| 3 |
| 4 |
解得BC=
8
| ||
| 3 |
AB=
| AC2-BC2 |
62-(
|
2
| ||
| 3 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
8
| ||
| 3 |
2
| ||
| 3 |
8
| ||
| 3 |
点评:本题考查了勾股定理,三角形的面积,三角形的中线的定义,利用勾股定理列出两个方程是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
异号两数相加,和为正数,则这两数中( )
| A、正数的绝对值较大 |
| B、负数的绝对值较大 |
| C、两个数的绝对值相等 |
| D、两个数的绝对值大小无法判断 |
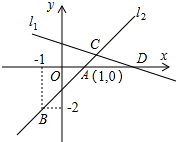 如图,直线l1的解析表达式为y=-
如图,直线l1的解析表达式为y=-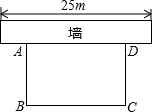 如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.
如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.