题目内容
18.在同一坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象回答以下问题:(1)直线y1=-2x+1、y2=2x-3与y轴分别交于点A、B,请写出A、B两点的坐标.
(2)写出直线y=-2x+1与y=2x-3的交点P的坐标.
(3)求△PAB的面积.
分析 (1)直接利用x=0求出y的值,进而得出A,B点坐标;
(2)直接利用函数图象得出其交点坐标;
(3)利用P,A,B的坐标得出△PAB的面积.
解答  解:(1)如图所示:当x=0时,y1=1,故A(0,1),
解:(1)如图所示:当x=0时,y1=1,故A(0,1),
当x=0时,y2=-3,故B(0,-3);
(2)如图所示:直线y=-2x+1与y=2x-3的交点P的坐标为:(1,-1);
(3)△PAB的面积为:$\frac{1}{2}$×AB×1=$\frac{1}{2}$×4×1=2.
点评 此题主要考查了一次函数图象画法以及三角形面积求法,正确画出函数图象是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7. 如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
 如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |

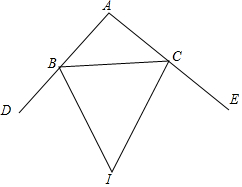 如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,
如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,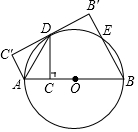 如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.