题目内容
2.若单项式$\frac{3}{8}$x5m+2n+2y3与-$\frac{2}{3}$x6y3m-2n-1的和仍是一个单项式,则m+n=$\frac{1}{2}$.分析 根据题意得到两单项式为同类项,利用同类项的定义求出m与n的值,即可求出m+n的值.
解答 解:∵单项式$\frac{3}{8}$x5m+2n+2y3与-$\frac{2}{3}$x6y3m-2n-1的和仍是一个单项式,
∴单项式$\frac{3}{8}$x5m+2n+2y3与-$\frac{2}{3}$x6y3m-2n-1为同类项,即$\left\{\begin{array}{l}{5m+2n=4①}\\{3m-2n=4②}\end{array}\right.$,
①+②得:8m=8,即m=1,
把m=1代入①得:n=-$\frac{1}{2}$,
则m+n=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 此题考查了同类项,熟练掌握同类项的定义是解本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
13.顺次连接平行四边形的各边中点,所得的图形一定是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 平行四边形 |
14. 数m、n在数轴上表示如图,下列判断正确的是( )
数m、n在数轴上表示如图,下列判断正确的是( )
 数m、n在数轴上表示如图,下列判断正确的是( )
数m、n在数轴上表示如图,下列判断正确的是( )| A. | |m|>1 | B. | n>-1 | C. | m+n=|m|-|n| | D. | m+n>0 |
11.若a>b,则下列不等式变形错误的是( )
| A. | 若a+1>b+1 | B. | -3a>-3b | C. | 3a-4>3b-4 | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
 如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.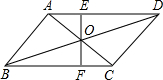 如图,?ABCD中,对角线AC与BD相交于O,EF是过点O的任一直线交AD于点E,交BC于点F,猜想OE和OF的数量关系,并说明理由.
如图,?ABCD中,对角线AC与BD相交于O,EF是过点O的任一直线交AD于点E,交BC于点F,猜想OE和OF的数量关系,并说明理由. 如图,AD∥BC,∠BAD=∠BCD,AE,CF分别是∠BAD,∠BCD的角平分线,由此判断AE∥CF,请说明理由.
如图,AD∥BC,∠BAD=∠BCD,AE,CF分别是∠BAD,∠BCD的角平分线,由此判断AE∥CF,请说明理由.