题目内容
16. 如图,在矩形ABCD中,AC是对角线,∠BAC的平分线交BC于点E,F是AB上一点.
如图,在矩形ABCD中,AC是对角线,∠BAC的平分线交BC于点E,F是AB上一点.(1)若∠ACD=60°,BE=1,求AC的长;
(2)若EF=EC,求证:AC=DC+BF.
分析 (1)先在RT△ABE中求出AB,再在RT△ABC中求出AC即可.
(2)先证明△AEB≌△AEH,再证明△EBH≌△EHC即可解决问题.
解答 解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠ABC=90°,
∴∠BAC=∠ACD=60°,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=30°,
在RT△ABE中,∵∠ABE=90°,BE=1,∠BAE=30°,
∴AB=$\sqrt{3}$BE=$\sqrt{3}$,
在RT△ABC中,∵∠ABC=90°,AB=$\sqrt{3}$,∠ACB=30°,
∴AC=2AB=2$\sqrt{3}$.
(2)延长AB使得BN=BF,连接EN,作EH⊥AC于H,
∵BF=BN,BE⊥FN,
∴EF=EN=EC,
在△AEB和△AEH中,
$\left\{\begin{array}{l}{∠EAB=∠EAH}\\{∠ABE=∠AHE=90°}\\{AE=AE}\end{array}\right.$,
∴△AEB≌△AEH,
∴BE=EH,AB=AH,
在RT△EBN和RT△EHC中,
$\left\{\begin{array}{l}{EB=EH}\\{EN=EC}\end{array}\right.$,
∴△EBN≌△EHC,
∴BN=HC,
∴AC=AH+HC=AB+NB=DC+BF.
点评 本题考查全等三角形的判定和性质、矩形的性质、直角三角形30度角的性质等知识,解题的关键是添加辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
6.分式方程$\frac{2}{x-2}$=1的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=0 |
7.已知ab2=-2,则-ab(a2b5-ab3+b)=( )
| A. | 4 | B. | 2 | C. | 0 | D. | 14 |
5.据报道,2015年国内生产总值达到677 000亿元,677 000用科学记数法表示应为( )
| A. | 0.677×106 | B. | 6.77×105 | C. | 67.7×104 | D. | 677×103 |
 如图所示,在△ABC中,在△ACB=90°,CD平分△ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.
如图所示,在△ABC中,在△ACB=90°,CD平分△ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.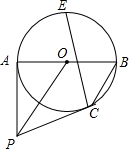 如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.