题目内容
7．
如图所示，在△ABC中，在△ACB=90°，CD平分△ACB，DE⊥AC于E，DF⊥BC于F，求证：四边形CEDF是正方形．
分析 根据有三个角是直角的四边形是矩形判定四边形CEDF是矩形，再根据正方形的判定方法即可得出结论．
解答 证明：∵CD平分∠ACB，DE⊥AC，DF⊥BC，
∴DE=DF，∠DFC=∠DEC=90°，
又∵∠ACB=90°，
∴四边形CEDF是矩形，
∵DE=DF，
∴矩形CEDF是正方形．
点评 本题考查正方形的判定、角平分线的性质和矩形的判定．要注意判定一个四边形是正方形，必须先证明这个四边形为矩形或菱形．
练习册系列答案
相关题目
如图，P是正方形ABCD内一点，将△ABP绕点B顺时针旋转90°，得到△CBP′，
如图，双曲线y=$\frac{k}{x}$（x＞0）经过点A与点B，且点A和点B的横坐标分别为a和2a（a＞0），若△AOB的面积为3，则k=4．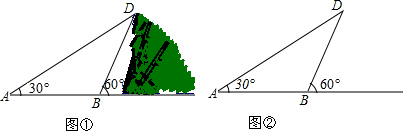
如图，D是AC上一点，DE∥AB，∠B=∠DAE，AD=AB，求证：AC=DE．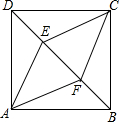
如图，正方形ABCD中，点E、F为对角线BD上两点，DE=BF，若BF=2，tan∠DAE=$\frac{1}{2}$，求四边形AECF的周长．
如图，在矩形ABCD中，AC是对角线，∠BAC的平分线交BC于点E，F是AB上一点．
如图，一次函数y=ax与反比例函数y=$\frac{k}{x}$的图象交于点A、B，点B的横坐标是5，OA=$\sqrt{26}$ 点P（m，n）（n＞1）是第一象限内y=$\frac{k}{x}$的图象上的动点，直线PA、PB分别交y轴于C、D．