题目内容
7．先化简，再求代数式$\frac{a}{{a}^{2}+2a+1}$÷（1-$\frac{1}{a+1}$）的值，其中a=tan60°-$\sqrt{2}$sin45°．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，利用特殊角的三角函数值求出a的值，代入计算即可求出值．
解答 解：原式=$\frac{a}{（a+1）^{2}}$÷$\frac{a+1-1}{a+1}$=$\frac{a}{（a+1）^{2}}$•$\frac{a+1}{a}$=$\frac{1}{a+1}$，
当a=tan60°-$\sqrt{2}$sin45°=$\sqrt{3}$-1时，原式=$\frac{\sqrt{3}}{3}$．
点评 此题考查了分式的化简求值，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
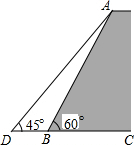如图，一堤坝的坡角∠ABC=60°，坡面长度AB=30米（图为横截面），为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得坡面的坡角∠ADB=45°，则此时应将坝底向外拓宽多少米？（结果保留到0.1米）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
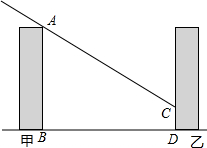有一朝向为正南方向的楼，该楼的一楼是高5米的小区超市，超市以上是居民区，在该楼的前面20米处要盖一栋高16米的甲楼，当冬季正午的阳光与水平线的夹角为32°时．
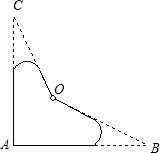一个零件的形状如图所示，按规定∠A，∠B，∠C的度数应为90°，21°，32°，产品检验员用工具测得∠BOC=140°，就判定这个零件不合格，为什么？
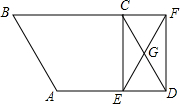如图，点E是平行四边形ABCD边AD上的一点，点G是CD的中点，连接EG并延长，交BC延长线于F，连接CE、DF．求证：四边形CEDF是平行四边形．
如图，A、B两点被池塘隔开，在AB外选一点C，连接AC和BC，怎样测出A，B两点间的距离？根据是什么？